Численное решение задачи на собственные значения для некоторых систем обыкновенных дифференциальных уравнений с полиномиальным слагаемым в дифференциальном операторе

Представлен явный численно-аналитический метод решения задачи на собственные значения для некоторых систем обыкновенных дифференциальных уравнений второго порядка с полиномиальным слагаемым в дифференциальном операторе, в частности, уравнений, описывающих связанные дырочные состояния в полупроводниковых квантовых ямах с полиномиальным профилем потенциала. Выполнен расчёт размерно-квантованных (связанных) состояний дырок в параболической GaAs квантовой яме. Вычислены законы дисперсии и волновые функции дырок для всех связанных состояний при изменении ширины квантовой ямы и величины потенциала.

1. ВВЕДЕНИЕ

В работе рассматриваются системы обыкновенных дифференциальных уравнений второго порядка вида:

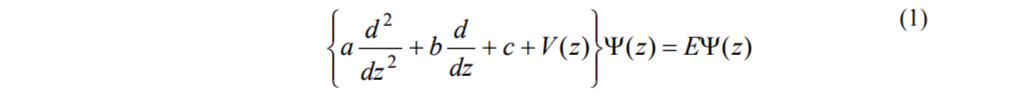
где a, b, c - это не зависящие от z n x n матрицы, матрица a - невырожденная эрмитова, матрица b - антиэрмитова, c - эрмитова; V(z) - полиномиальная, вообще говоря, матричная функция (потенциал), Y - это n-компонентный вектор решений (волновая функция); E - параметр (энергия), который может быть действительным [Galiev, 2002], или комплексным [Polupanov, 2008].

К решению задачи на собственные значения и задачи рассеяния для уравнения (1) сводятся многие прикладные проблемы квантовой механики, в частности - в рамках приближения эффективной массы [Luttinger, 1956] - проблема размерно-квантованных состояний и состояний рассеяния электронов и дырок в полупроводниковых квантовых ямах (КЯ) при наличии внешних полей. В данной работе мы будем рассматривать решение задачи на собственные значения для уравнения (1) и его применение к исследованию размерно-квантованных состояний дырок в КЯ. Следует отметить, что даже в простейшем случае одного уравнения (n = 1 в (1)), когда потенциал V(z) не есть кусочно-постоянная функция, для нахождения энергий связанных состояний и соответствующих волновых функций используются различные, существенно приближённые численные методы. Например, приближение многоступенчатого потенциала [Ando, 1987], кусочно-линейного потенциала [Lui, 1986], методы конечных элементов [Nakamura, 1989], вариационный метод [Bastard, 1983]. В случае системы уравнений (n > 1 в (1)) обычно использовались конечно-разностные методы [Polupanov, 1985], которые могут давать большую погрешность даже в случае одного уравнения. Значительно более эффективными и точными являются методы, основанные на численном интегрирования дифференциальных уравнений [9-10]. В настоящей работе представлен вариант явного численно-аналитического метода рекуррентных последовательностей решения задачи на собственные значения, предложенного в [Ikonic, 1992], развитого в случае сингулярной задачи на собственные значения в [11, 12] и систем вида (1) в [Chuang, 1991].

2. ОБЩАЯ ФОРМУЛИРОВКА МЕТОДА

Для дальнейшего анализа удобно записать систему уравнений (1) в виде системы уравнений первого порядка, заменяя функцию 2п-компонентной функцией y(z) следующего вида

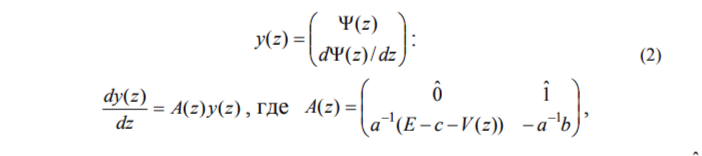
A(z) - это матричная функция размером 2n х 2n, построенная из матриц a, b, c, нулевой 0 и единичной î матриц, размером n х n, функции V(z) и энергии E.

Мы рассматриваем случай кусочно-полиномиальной функции V (z) (потенциала КЯ), тогда функция V(z) - это полином степени n по z при 0 < z < d и V(z) = 0 пр z □ 0, z ≥ d. Матричную функцию A (z) можно представить в виде

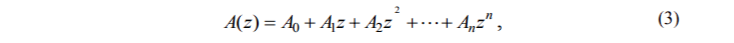
где A_i, (i=0,1,...,n) -это постоянные 2n х 2n матрицы (вообще говоря, различные при 0 ≤ z ≤ d при z < 0, z > d).

Рассматривается следующая задача на собственные значения для уравнения (2) (а, значит, и (1)). Необходимо найти такие дискретные значения параметра E (E=Ei, i=0,1,...), при которых выполняются следующие условия для соответствующих им решений:

1. y(z) → 0 при z - ± ∞

2. y(z) непрерывна пр z = 0 и z = d.

Необходимо также найти соответствующие со бственные функции - нормированные решения (1) Ψ_E(z). Отметим, что в приложениях возможны и более общие ограниченные условия, чем 2), например, если матрицы a, b, c разрывно изменяются при прохождении точек z = 0, z =

d (см., например, [Федорюк, 1985]). Для определённости, но без потери общности, мы будем использовать условие 2).

Рассмотрим решения (фундаментальную систему решений) (2) по отдельности при 0 ≤ z ≤ d, z < 0 и z > d.

Поскольку предполагается , что функция V(z) - это многочлен (3) при 0 < z < d, то следующий ряд для каждого отдельного решения из фундаментальной системы решений

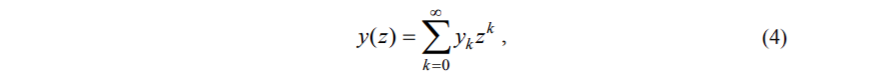
где у_k - не зависящие от z 2n-векторы (столбцы из 2n элементов), сходится на этом отрезке (см. [ 1 5 ] ) , т. е . каждое решение уравнения (2) можно представить в виде сходящегося ряда (4). Подставляя (3) и (4) в уравнение (2), получаем следующие рекуррентные соотношения для векторов yk:

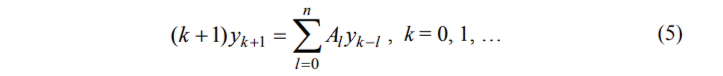
и У₀ - это некоторый заданный столбец из 2n элементов.

Поскольку рассматривается польномиальная функция V(z), то выражения (4) и (5) дают точные формулы для решений (2) при 0 ≤ z ≤ d и позволяют вычислить эти решения с любой требуемой точностью, обрыв я соответствующие ряды при достаточно большой величине k = k_max.

С учетом того, что при z < 0 и z > d функция V(z) = 0, имеем следующее уравнение при z < 0, z > d: 

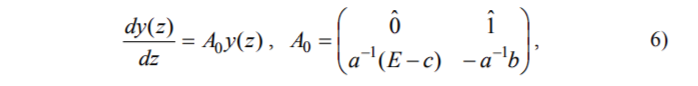
Решения уравнения (6), удовлетворяющие граничным условиям при z → ±∞, легко найти, поскольку они есть суперпозиции 2n-столбцов (собственных векторов матрицы А0), умноженных на экспоненциальные функции с, вообще говоря, комплексными аргументами, соответствующими собств нным зн чениям матрицы A₀. В случае решения задачи на собственные нужно рассматривать те значения параметра E (энергии), при которых собственные значения матрицы A₀ имеют не равную нулю действительную часть и при этом следует учитывать только те экспоненциальные функции в решениях, которые убывают при z  → ±∞.

3. РЕШЕНИЕ ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ В СЛУЧАЕ СИСТЕМЫ ДВУХ ОДУ ВТОРОГО ПОРЯДКА

 

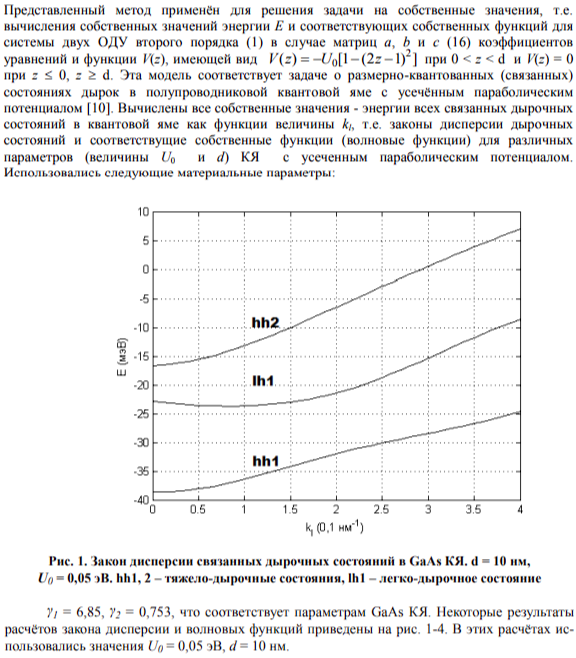
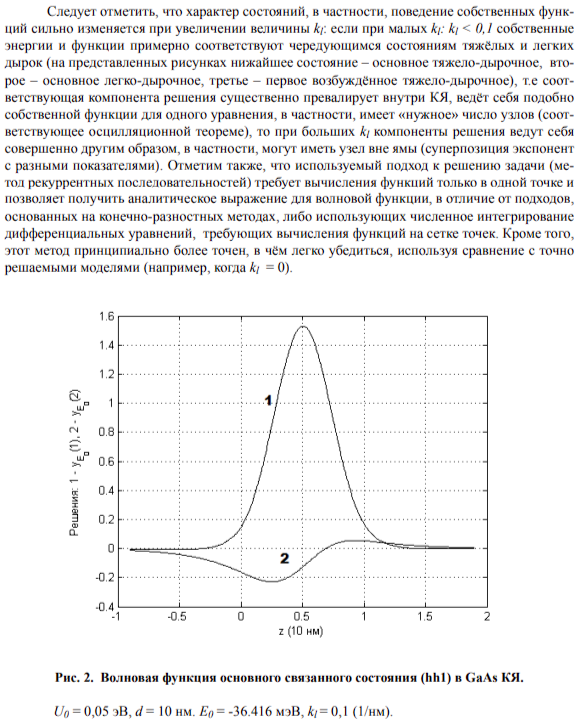
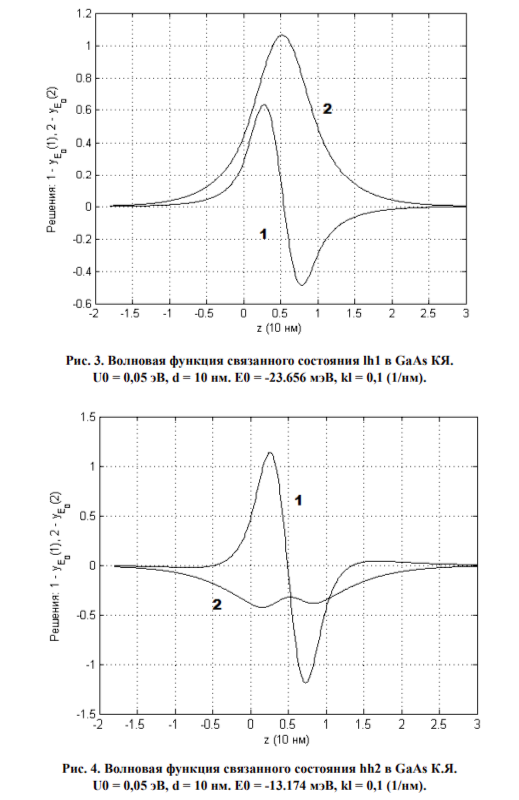
4. РЕЗУЛЬТАТЫ РАСЧЕТОВ И ОБСУЖДЕНИЕ

1. Galiev V.I., Kruglov A.N., Polupanov A.F., Goldys E., Tansley T., Multichannel carrier scattering at quantum-well heterostructures, Semiconductors , 2002, 36 (5), pp. 546-551.
2. Polupanov A.F., Galiev V.I., Kruglov A.N. The over-barrier resonant states and multi- channel scattering by a quantum well. Int. Jnl. of Multiphysics, 2008, 2 (2), pp. 171-177
3. Luttinger J.M., Quantum theory of cyclotron resonance in semiconductors: General Theory. Phys. Rev., 1956, 102 (4), pp. 1030-1041.
4. Ando Y., Itoh T., J. Appl. Phys., 1987, Vol. 61, pp. 1497-1501
5. Lui W.W., Fukuma M., J. Appl. Phys., 1986, Vol. 60, pp. 1555-1561
6. Nakamura K., Shimizu A., Koshiba M., Hayata K., IEEE J. Quant. Electr., 1989, Vol. 25, pp. 889-894
7. Bastard G., Mendez E.E., Chang L., Esaki L., Phys. Rev., 1983, Vol. B28, pp. 3241-3245 8. Ahn D., Chuang S.L., J. Appl. Phys., 1988, Vol. 64, pp. 4056-4060
8. Polupanov A.F., Energy spectrum and wave functions of an electron in a surface energy well in a semiconductor, Sov. Phys. Semicond., 1985, Vol. 19 (9), 1013-1015.
9. Ikonic Z., Milanovic V., Hole-bound-state calculation for semiconductor quantum wells. Phys. Rev., 1992, Vol. B45, pp. 8760-8762
10. Galiev V.I., Polupanov A.F., Shparlinski I.E., On the construction of solutions of systems of linear ordinary differential equations in the neighbourhood of a regular singularity, Journal of Computational and Applied Mathematics, 1992, Vol. 39, pp. 151 - 163.
11. Galiev V.I., Polupanov A.F., Accurate solutions of coupled radial Schrödinger equations, J.Phys. A: Math. Gen., 1999, Vol. 32, pp. 5477-5492.
12. Galiev V.I., Goldys E., Novak M.G., Polupanov A.F., Tansley T. Superlattices and Microstruc- tures. 1995, Vol. 17, pp. 389-481.
13. Chuang S.L., Efficient band-structure calculations of strained quantum wells. Phys. Rev. B, 1991, Vol. 43 (12), pp. 9649-9661.
14. Федорюк М.В. Асимптотические методы линейных обыкновенных дифференциальных уравнений. М. Наука, 1985.
15. Broido D.A., Sham L.J., Effective masses of holes at GaAs-AlGaAs heterojunctions. Phys. Rev. B, 1985, Vol. 31 (2), pp. 888-892.