В работе предложен алгоритм, позволяющий находить оптимальное программное управление с помощью метаэвристических мультиагентных методов условной глобальной оптимизации [Пантелеев, 2016]: метода, имитирующего поведение стаи рыб; метода, имитирующего популяцию криля; метода, имитирующего империалистическую конкуренцию, описанных в [Каранэ, 2018]. Эти методы основаны на процессах, происходящих в среде, имеющей множество агентов. Агенты имеют возможность обмениваться информацией для того, чтобы найти решение задачи. На основе данных алгоритмов разработано программное обеспечение в среде Microsoft Visual Studio. Оно позволяет находить оптимальное программное управление динамическим системами, линейными по ограниченному управлению, в релейном виде, а также соответствующие траектории и наилучшее значение критерия. По результатам решения специально подобранного набора тестовых задач о нахождении оптимального программного управления [Финкельштейн, 2018] можно сделать вывод о том, что рассмотренный алгоритм можно успешно применять и находить близкое к точному решение за приемлемое время.
1. ПОСТАНОВКА ЗАДАЧИ
Пусть поведение модели объекта управления описывается обыкновенным дифференциальным уравнением

Для систем (1) , линейных по управлению, структура оптимального программного управления согласно принципу максимума является релейной. Поэтому предлагается искать приближенное решение в параметрическом виде, определяемом числом моментов переключения управления и их значениями.
2. АЛГОРИТМ ПОИСКА ОПТИМАЛЬНОГО ПРОГРАММНОГО УПРАВЛЕНИЯ


3. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ
На основе изложенного алгоритма было разработано программное обеспечение. Для его создания использовалась среда разработки Microsoft Visual Studio, язык программирования C#.
На главной форме (рис. 1) метода пользователь может выбрать задачу для нахождения оптимального программного управления, задать количество переключении в управлении, выбрать метод оптимизации и указать его параметры.
Результатом работы программы являются координаты точек x1(t1), x2(t1), оптимальное значение функционала I и координаты точек переключения. По окончании поиска оптимального управления программа изображает графики функции управления и траектории.
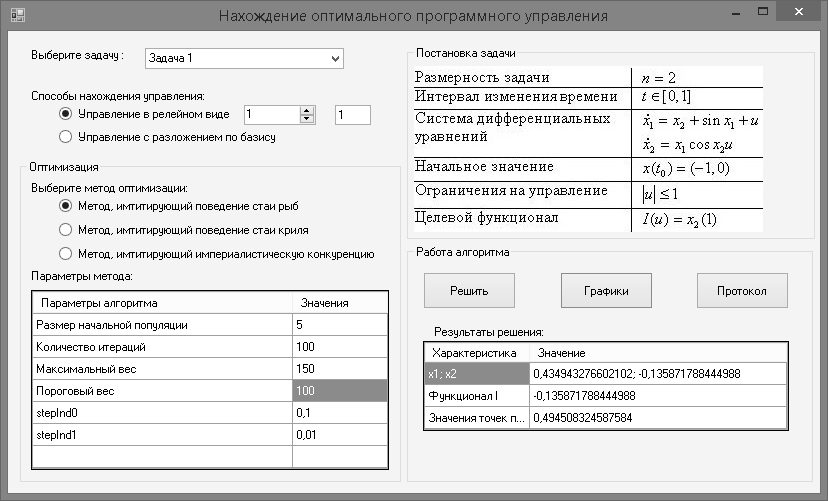
Рис. 1 Общий вид интерфейса программы
4. РЕШЕНИЕ ЗАДАЧ ПОИСКА ОПТИМАЛЬНОГО ПРОГРАММНОГО УПРАВЛЕНИЯ
Задача 1 [Финкельштейн, 2018]. Постановка задачи (табл. 1):
Таблица 1. Постановка задачи 1
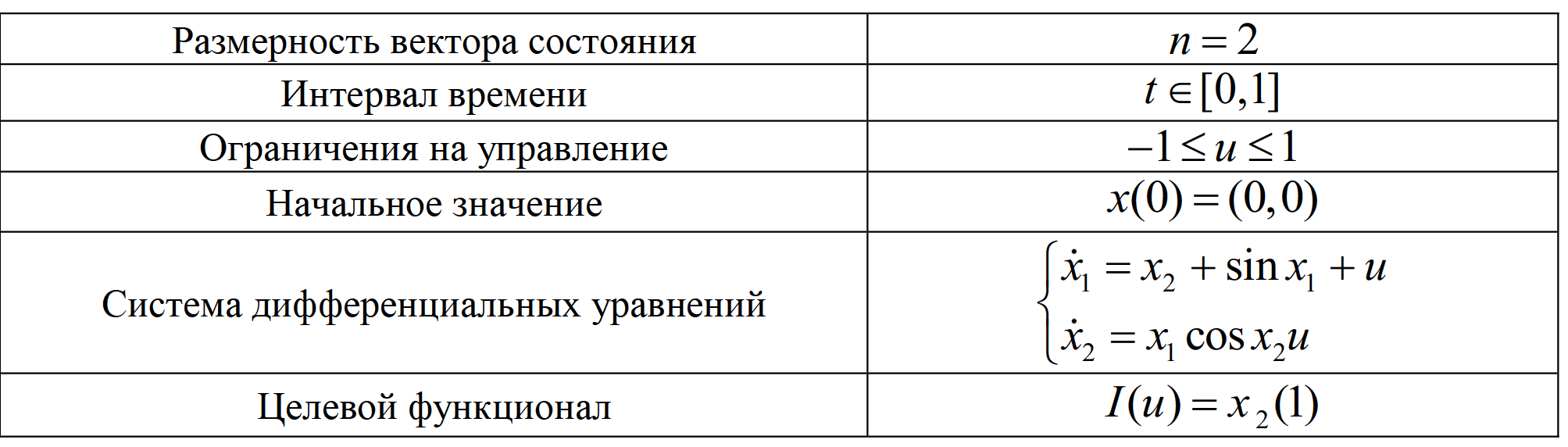

Таблица 2. Результаты решения задачи 1
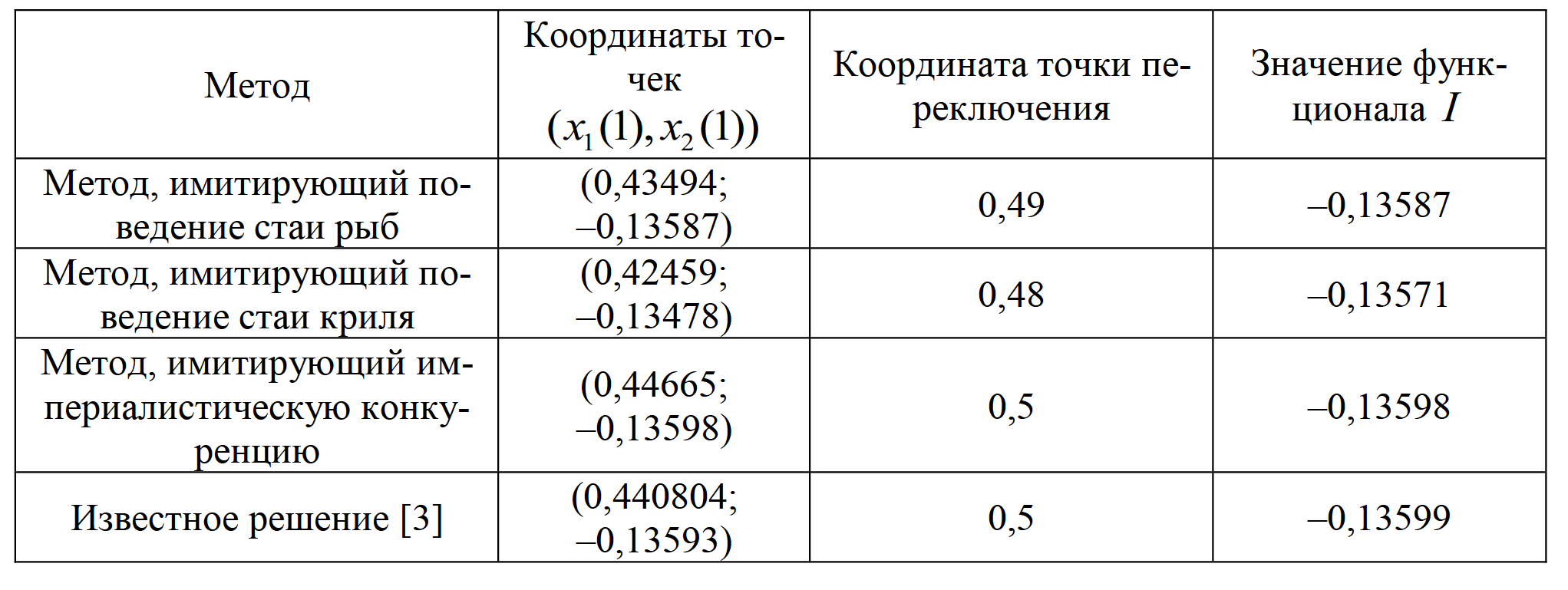
Графики оптимальных траекторий и управления представлены на рис. 2:
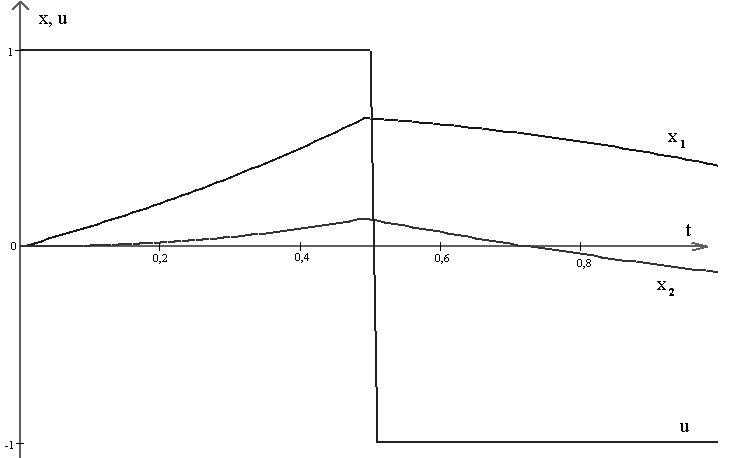
Рис. 2 Графики оптимальных траекторий и управления
Задача 2 [Финкельштейн, 2018]. Постановка задачи (табл. 3):
Таблица 3. Постановка задачи 2


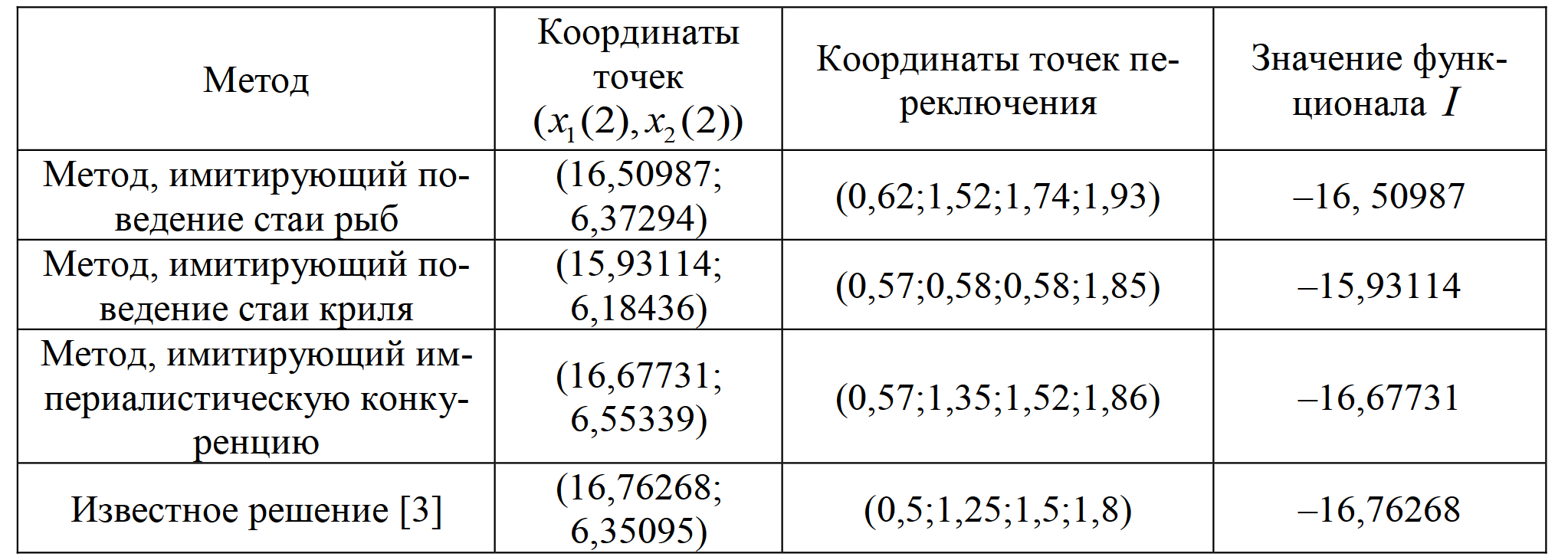
Таблица 4. Результаты решения задачи 2
Графики оптимальных траекторий и управления представлены на рис. 3:
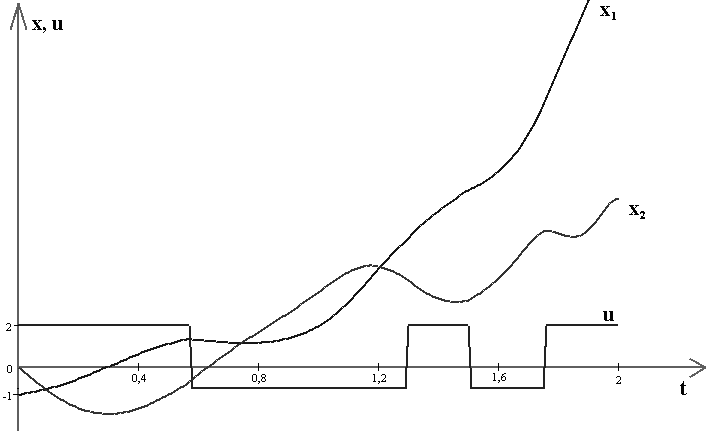
Рис. 3 Графики оптимальных траекторий и управления
Задача 3 [Финкельштейн, 2018]. Постановка задачи (табл. 5):
Таблица 5. Постановка задачи 3


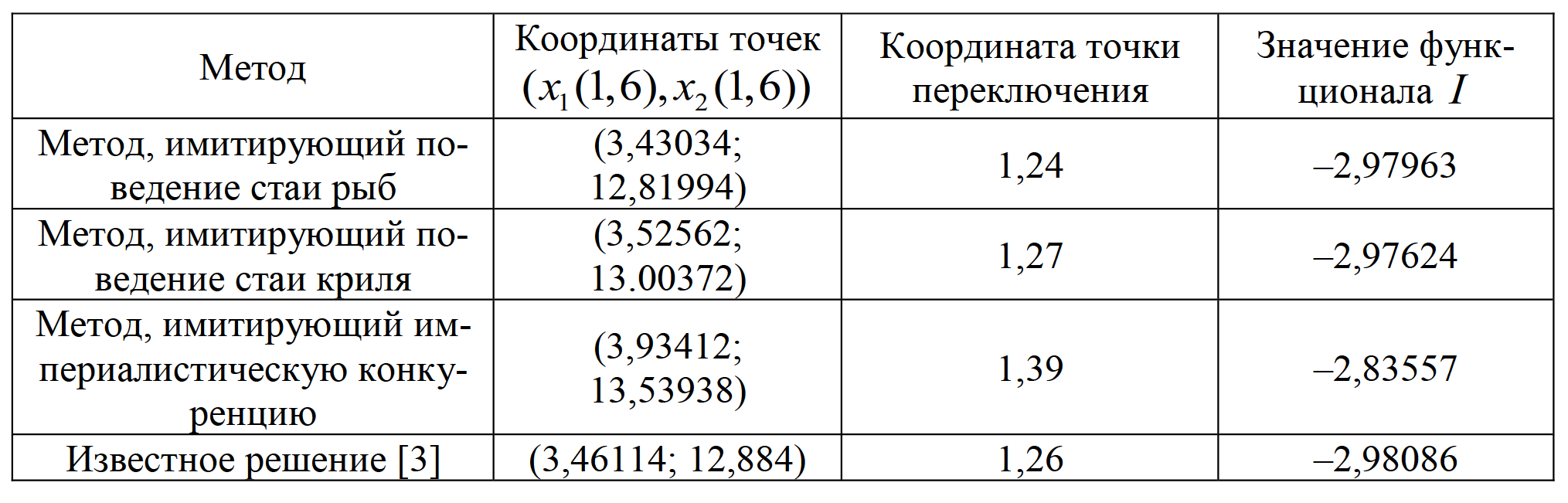
Таблица 6. Результаты решения задачи 3
Графики оптимальных траекторий и управления представлены на рис. 4:
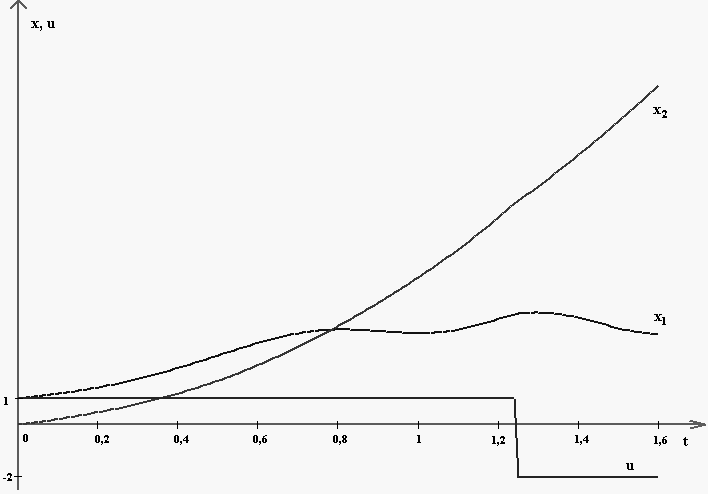
Рис. 4 Графики оптимальных траекторий и управления
ЗАКЛЮЧЕНИЕ
Разработанный алгоритм позволяет находить оптимальное программное управление с помощью мультиагентных метаэвристических методов условной глобальной оптимизации. Он позволяет решать задачи, в которых кроме глобального экстремума имеются один или несколько локальных, за приемлемое время.