Градиентные методы оптимизации в машинном обучении идентификации параметров динамических систем

В статье рассматривается один из возможных способов решения задачи оценки неизвестных параметров динамических моделей, описываемых дифференциально–алгебраическими уравнениями. Оценка параметров производится по результатам наблюдений за поведением математической модели. Их значения находятся в результате минимизации критерия, описывающего суммарное квадратическое отклонение значений координат вектора состояния от полученных при измерениях точных значений в различные моменты времени. На значения параметров наложены ограничения параллелепипедного типа. Для решения задачи оптимизации предлагается использовать градиентные методы оптимизации, используемые в процедурах машинного обучения: метод стохастического градиентного спуска, классический метод моментов, ускоренный градиентный метод Нестерова, метод адаптивного градиента, метод скользящего среднего, метод адаптивной оценки моментов, модификация метода адаптивной оценки, ускоренный по Нестерову метод адаптивной оценки. Приведен пример идентификации параметров линейной математической модели, описывающей изменение__ характеристик химического процесса, на котором продемонстрирована сравнительная эффективность методов оптимизации выбранной группы. Применяемые методы поиска экстремума не гарантируют нахождения результата – глобального экстремума, но позволяют получать решение достаточно хорошего качества за приемлемое время. Приведены результаты расчетов всеми перечисленными методами оптимизации, даны рекомендации по выбору параметров методов. Полученные численные результаты продемонстрировали эффективность предложенного подхода. Найденные приближенные значения оцениваемых параметров незначительно отличаются от лучших известных решений, полученных другими способами.

В статье рассматривается один из возможных способов решения задачи оценки неизвестных параметров динамических моделей, описываемых дифференциально-алгебраическими уравнениями. Оценка параметров производится по результатам наблюдений за поведением математической модели. Их значения находятся в результате минимизации критерия, описывающего суммарное квадратическое отклонение значений координат вектора состояния от полученных при измерениях точных значений в различные моменты времени. На значения параметров наложены ограничения параллелепипедного типа. Для решения задачи оптимизации предлагается использовать градиентные методы оптимизации, используемые в процедурах машинного обучения: метод стохастического градиентного спуска, классический метод моментов, ускоренный градиентный метод Нестерова, метод адаптивного градиента, метод скользящего среднего, метод адаптивной оценки моментов, модификация метода адаптивной оценки, ускоренный по Нестерову метод адаптивной оценки. Приведен пример идентификации параметров линейной математической модели, описывающей изменение характеристик химического процесса, на котором продемонстрирована сравнительная эффективность методов оптимизации выбранной группы. Применяемые методы поиска экстремума не гарантируют нахождения результата - глобального экстремума, но позволяют получать решение достаточно хорошего качества за приемлемое время. Приведены результаты расчетов всеми перечисленными методами оптимизации, даны рекомендации по выбору параметров методов. Полученные численные результаты продемонстрировали эффективность предложенного подхода. Найденные приближенные значения оцениваемых параметров незначительно отличаются от лучших известных решений, полученных другими способами.

Введение

Задача нахождения оценок параметров динамических моделей имеет достаточно длинную историю. Большинство работ в этой области основано на вероятностном подходе, когда оценка неслучайного параметра является случайной величиной из-за проявления различных факторов. Существуют методы для построения точечных оценок, например, метод максимального правдоподобия. Как правило, при их применении исследуются статистические свойства этих оценок: несмещённость, сходимость к точному значению. Во многих случаях недостаточно иметь только точечные оценки, поэтому необходимо знать, в каких пределах находится точное значение параметра с заданной надёжностью, что связано с проблемой построения доверительных интервалов. Все перечисленные подходы основаны на том, что имеется какая-то информация об исследуемом явлении, например, известны наблюдения за реализацией случайной величины, т.е. задана выборка. На основе этой информации разрабатывались алгоритмы для построения оценок [1].

Другим направлением исследований является применение прямых методов оптимизации. В данной работе рассматривается математическая модель динамической системы с неизвестными параметрами, описываемая системой дифференциальных уравнений. На каждый параметр могут быть наложены ограничения в виде отрезка с фиксированными концами. Известны результаты наблюдения за состоянием системы в определённые моменты времени функционирования системы. Целевая функция характеризует сумму квадратов отклонений значений всех компонент решения системы дифференциальных уравнений в заданные моменты времени от полученных в результате измерений значений координат вектора состояния модели. Ставится задача минимизации целевой функции на множестве возможных значений параметров, удовлетворяющих заданным ограничениям. Для решения таких задач существует множество классических методов нулевого, первого и второго порядков [2], однако их реализация может быть связаны с завышенными требованиями к элементам постановки задачи. Альтернативой является применение метаэвристических алгоритмов [3, 4], которые позволяют получить решение достаточно хорошего качества за приемлемое время. В то же время, с ростом числа переменных решение требует значительных вычислительных ресурсов.

Поскольку в данном случае задача оценивания неизвестных параметров похожа на задачу линейной регрессии, которая может быть решена с помощью алгоритмов машинного обучения, то предлагается применить методы этой распространенной группы [5].

Кроме того, наблюдения о координатах вектора состояния модели получаются в ходе физических измерений, поэтому есть все основания предполагать, что они производятся с ошибкой, а целевая функция имеет смысл среднего квадратичного отклонения.

Применены следующие градиентные методы оптимизации: метод стохастического градиентного спуска (Stochastic Gradient Descent, SGD), классический метод моментов (Classical Momentum), ускоренный градиентный метод Нестерова (Nesterov Accelerated Gradient, NAG), метод адаптивного градиента (Adaptive Gradient, AdaGrad), метод скользящего среднего (Root Mean Square Propagation, RMSProp), метод адаптивной оценки моментов (Adaptive Moment Estimation,Adam), модификация метода Adam (Adamax), ускоренный по Нестерову метод адаптивной оценки моментов (Nesterov-accelerated Adaptive Moment Estimation, Nadam). Они позволяют найти приближённое решение за приемлемое время при работе с большими данными. Как правило, методы имеют много параметров, которые необходимо выбрать, и для разных задач эти параметры могут отличаться. В работе предложены некоторые рекомендации по выбору параметров этих методов.

Постановка задачи

Алгоритмы решения задачи

Стратегия поиска решения задачи оценки параметров

Для нахождения неизвестных параметров необходимо решить задачу условной оптимизации (1). Сложность задачи заключается в том, что целевая функция зависит от решения системы дифференциальных уравнений (2). Если система линейная, то удаётся найти аналитическое решение, что позволяет находить производные целевой функции по параметру и пользоваться градиентными методами оптимизации процедур машинного обучения. Если система нелинейная, то рекомендуется либо применять методы нулевого порядка (адаптивный метод случайного поиска, метод случайного поиска с последовательной редукцией области исследования [3]), либо использовать конечно-разностные аппроксимации для нахождения частных производных по параметрам.

Пример решения задачи оценки параметров

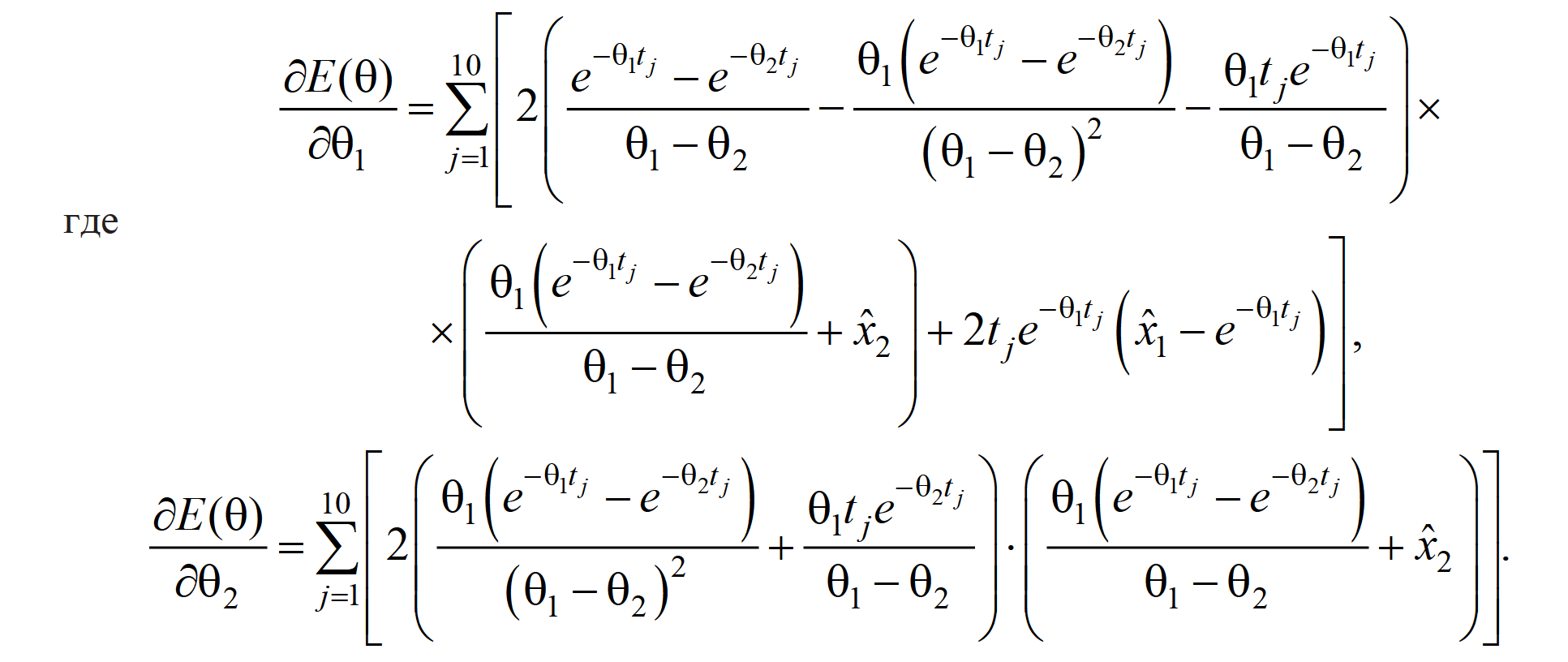
На рис. 1 приведены результаты решения примера (изменение целевой функции с ростом числа итераций) при разных значениях параметров методов. Видно, что все описанные методы сходятся к наилучшему ответу, но скорость сходимости разная. Результаты решения примера позволяют определить наиболее эффективный метод при заданном шаге и одинаковом количестве итераций: метод Adam быстрее всех сходится при наименьшем шаге, равном 0,2 .

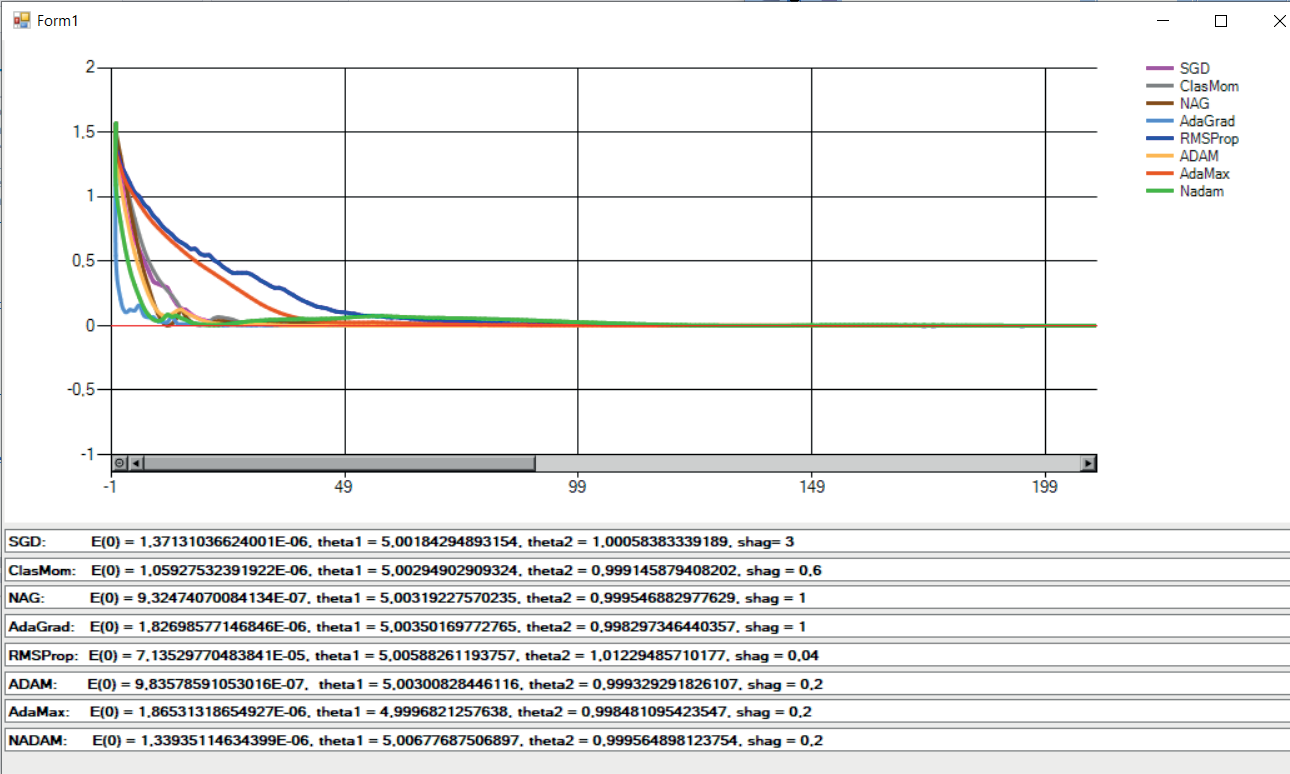
Рис. 1 а. Результаты применения градиентных методов

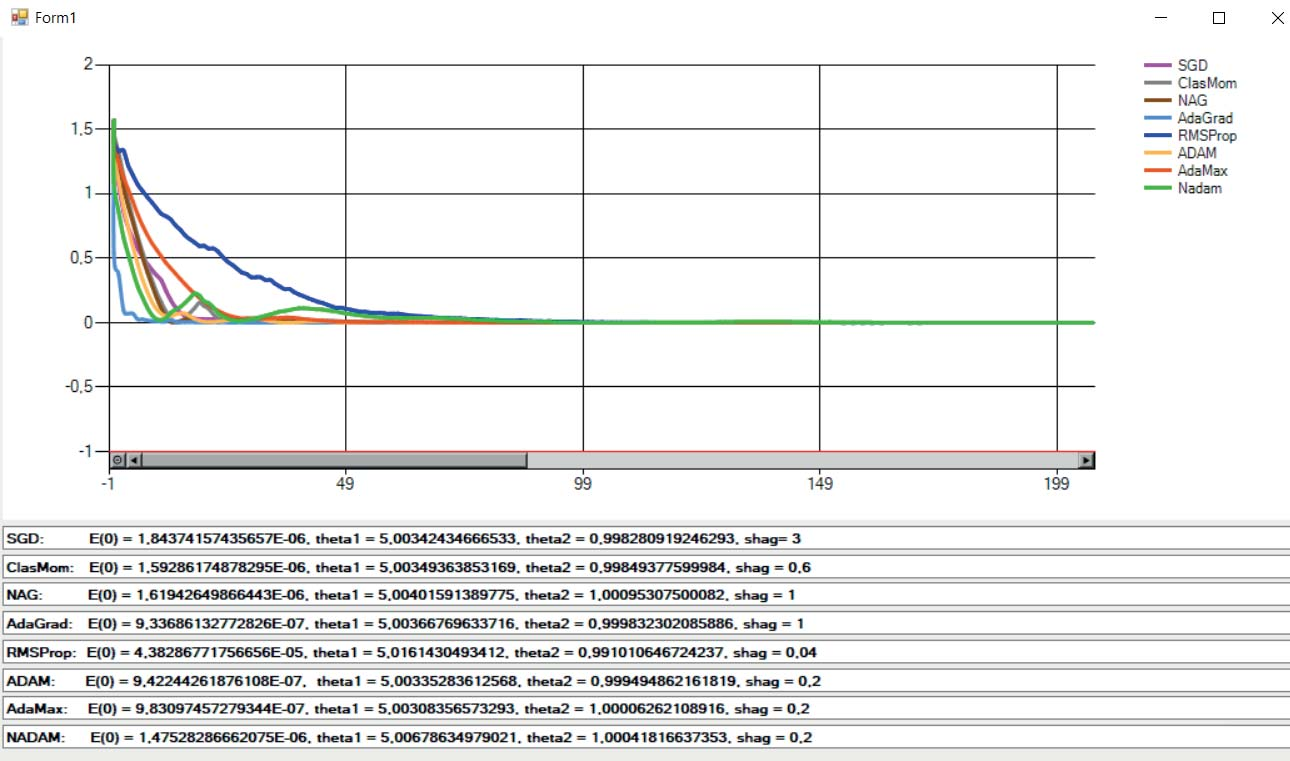
Рис. 1 б. Результаты применения градиентных методов

Заключение

Сформированы алгоритмы решения задачи оценивания параметров динамических систем с применением градиентных методов оптимизации в машинном обучении: SGD, Classical Momentum, NAG, AdaGrad, RMSProp, Adam, Adamax, Nadam. Решен модельный пример оценивания параметров химической системы: модели протекания необратимой реакции первого порядка. Проведен сравнительный анализ эффективности алгоритмов оптимизации.

1. Ивченко Г.И., Медведев Ю.И. Введение в математическую статистику.– М.: Книжный дом «ЛИБРОКОМ», 2014. 352 c.
2. Пантелеев А.В., Летова Т.А. Методы оптимизации. Практический курс: учебное пособие/А.В.Пантелеев, Т.А.Летова.– М.: Логос, 2011.
3. Пантелеев А.В., Скавинская Д.В. Метаэвристические алгоритмы глобальной оптимизации.–М.: Вузовская книга, 2019.
4. Пантелеев А.В., Крючков А.Ю. Метаэвристические методы оптимизации в задачах оценки параметров динамических систем // Научный вестник Московского государственного технического университета гражданской авиации. 2017. 20. № 2. С. 37–45.
5. Ruder S. An Overview of Gradient Descent Optimization Algorithms arXiv:1609.04747v2 [cs.LG] 15 Jun 2017.
6. Floudas C.A., Pardalos P.M., Adjimann C.S., Esposito W.R., Gumus Z.H., Harding S.T., Schweiger C.A. Handbook of test problems in local and global optimization, 1999. Vol. 67. Springer US. 442 p. https://titan.princeton.edu/TestProblems/
7. Tjoa I.–B., Biegler L.T. Simultaneous solution and optimization strategies for parameter estimation of differential–algebraic equation systems. Industrial & Engineering Chemistry Research, 1991, Vol. 30, No. 2, pp. 376–385. https://doi.org/10.1021/ie00050a015

PlumX

Метрики публикации