Введение
Задачи и методы нахождения управления составляют основу современной теории управления [1-6]. Они дополняют классические постановки задач синтеза оптимальных законов управления по различным критериям. При решении различных задач в данной области обычно применяется метод пространства состояний, частотный подход и метод линейных матричных неравенств [7-13]. Задача робастного оценивания координат вектора состояния по результатам измерений изучалась в [14-22]. Среди них выделим работу [Banavar] , в которой с помощью применения принципа максимума и игрового подхода найдены соотношения, определяющие матрицу коэффициентов усиления наблюдателя и наихудшие законы изменения возмущений и погрешностей как функции времени. В [Li, а] для решения игровой задачи предложено использовать обучение с подкреплением. Приложение теории построения робастных наблюдателей в задачах управления летательными аппаратами рассмотрено в [24,25].
В данной статье сформулированы достаточные условия синтеза наблюдателя. Доказательство построено на основе принципа расширения [26-28]. Это позволило получить выражения для управления процессом оценки вектора состояния и законы наихудшего противодействия со стороны внешних воздействий и погрешностей измерения в форме обратных связей по ошибкам оценивания. С применением полученных соотношений решены две задачи оценивания вектора состояния самолетов для нестационарной модели с конечным временем функционирования и для стационарной модели с полубесконечным временем [Chang J.-L, 2018].
Постановка задачи
Заданы математическая модель объекта управления
(1)
и модель измерительной системы
(2)
где вектор состояния, вектор возмущений, вектор выхода (вектор измерений), вектор ошибок и погрешностей измерений, время, заданное положительное число. Заданы непрерывные матрицы , размеров соответственно.
Предполагается, что:
а), ,
б) ;
в) невырожденная матрица.
Ставится задача о нахождении оценки вектора состояния по результатам накопленной информации, полученной от измерительной системы, т.е. . При этом требуется минимизировать величину ошибки оценивания в условиях неопределенности информации о векторе начальных состояний , законах изменения векторов возмущений и ошибок измерений.
Предположим, что структура наблюдателя состояния описывается уравнением
, (3)
где вектор оценок координат вектора состояния, неизвестная непрерывная матрица размеров вектор начальных значений оценок координат вектора состояния, задаваемый исходя из имеющейся априорной информации о возможных начальных состояниях модели объекта управления (1). Матрица выполняет функцию управления процессом наблюдения.
Получим уравнение, описывающее изменение ошибки оценивания, вычитая из уравнения (1) уравнение (3) с учетом (2) и обозначения :
,
, . (4)
Далее для упрощения записи зависимость матриц математической модели от времени опущена. Также будет использоваться обозначение взвешенной нормы где заданная положительно полуопределенная симметрическая матрица.
Требуется обеспечить (если это возможно) выполнение неравенства:
(5)
где симметрические положительно определенные матрицы соответствующих размеров, заданное неотрицательное число. При этом желательно найти минимальное значение , при котором указанные свойства еще справедливы, минимизируя значение числителя дроби при одновременной максимизации знаменателя.
Иными словами, функционал качества управления наблюдателем состояния должен удовлетворять условию
, (6)
которое будет выполняться при минимизации затрат на управление процессом оценивания при наихудшем влиянии возмущений, начального состояния и ошибок измерений. Множитель ½ добавлен для уменьшения громоздкости записи после дифференцирования.
Требуется найти наилучшую матрицу наблюдателя (3), наихудшие законы управления внешним воздействием и погрешностью измерений , наихудший вектор начальных состояний , обеспечивающие выполнение условия (6).
Синтез наблюдателей состояния
Сформулируем поставленную задачу как игровую, где первый игрок – матрица , выбирается при каждом из условия минимизации значения функционала, а второй игрок ‑ составной вектор , из условия его максимизации:
. (7)
Будем считать, что второй игрок при фиксированном действии первого игрока стремится максимизировать величину функционала, характеризующую интегральную ошибку оценивания. Поэтому сначала рассмотрим задачу максимизации функционала по , или, что то же самое, минимизации функционала, отличающегося знаком:
(8)
Будем использовать достаточные условия оптимальности В.Ф.Кротова [26,27] для задачи
,
где – вектор состояния системы, – вектор управления, – некоторое заданное множество; – время, – промежуток времени функционирования системы, моменты времени и заданы, ; внешние воздействия на объект управления отсутствуют, – непрерывно дифференцируемая функция; множество допустимых процессов, т. е. множество пар образуемых траекториями и управлениями , в которых , функции непрерывны и кусочно-дифференцируемы, а кусочно-непрерывны, удовлетворяют дифференциальному уравнению системы и начальному условию.
Утверждение (частный случай достаточных условий оптимальности [26,27]). Для того чтобы элемент был минималью, достаточно существования такой функции , чтобы выполнялись два условия:
- ,
где
(9)
(10)
Функцию и величину без ограничения общности можно положить равными нулю. При этом минимальное значение функционала .
Доказательство. Применим принцип расширения [26-28]. Определим множество пар где элементы пар по сравнению с входящими в множество необязательно связаны дифференциальным уравнением , , допускаются разрывы первого рода функций на множестве . Таким образом, множество и расширение построено.
Доопределение функционала на множестве производится с помощью задания функции . На множестве определим функционал: .
На множестве , где между функциями существует дифференциальная связь, с учетом равенства справедливо
и поэтому
Таким образом, на множестве функционалы и совпадают. Поведение функционала на множестве полностью определяется выбором функции .
Пусть имеется функция . Найдем минимум функционала на множестве . Операции нахождения экстремума в первых двух слагаемых могут быть выполнены по отдельности в силу свойств функций , образующих пары . Тогда .
Из условий 1) и 2) следует, что , т.е. .Поскольку , то . Но на множестве справедливо тождество . Поэтому , что соответствует определению минимума функционала на множестве .
Если существует функция , удовлетворяющая условиям 1), 2) утверждения при то, применяя прямую подстановку в , , можно показать, что функция также удовлетворяет этим условиям при , . В этом случае из доказанного утверждения и выражения для следует .
Доказательство закончено.
Замечание 1. В решаемой задаче .
Пусть имеется функция . Составим конструкции (9),(10) для функционала (8) и модели динамической системы, описываемой уравнением (4) для ошибки оценивания:
(11)
где .
Используем правила векторного дифференцирования [Бортаковский, 2010]: (если матрица симметрическая, то ), и свойства операции транспонирования .
Найдем максимум функции по переменным , используя необходимые условия безусловного экстремума: , .
Отсюда
, . (12)
Проверим выполнение достаточных условий максимума: ,
так как , , а определитель блочно-диагональной матрицы равен произведению определителей блоков.
Тогда
Так как для матриц-столбцов справедливо равенство , то можно использовать правила нахождения матричных градиентов [Гроп, 1979]: .
Заметим, что .
Тогда
Отсюда
(13)
Будем искать функцию в форме
, (14)
где неизвестная симметрическая матрица порядка .
Тогда и из (12),(13) получаем
, , (15)
(16)
Запишем равенство 1) из достаточных условий оптимальности с учетом , подставляя в выражение вместо формулу (16), т.е.
Используя условие равенства нулю квадратичной формы , получаем
С учетом равенства имеем и . Тогда, умножая уравнение на матрицу слева и справа, получаем
или (17)
Выпишем условие 2) из достаточных условий оптимальности
Отсюда следует граничное условие для уравнения (17):
. (18)
Частный случай (линейные стационарные системы с полубесконечным промежутком функционирования).
Рассмотрим случай, когда матрицы системы (1),(2) не зависят от , а момент окончания процесса функционирования системы :
Структура наблюдателя состояния (3) имеет вид .
Требуется обеспечить (если это возможно) выполнение неравенства:
где симметрические положительно определенные матрицы соответствующих размеров, заданное неотрицательное число.
Тогда
(19)
, ,
где матрица положительно определенное решение алгебраического уравнения Риккати
(20)
Замечание 2. В правую часть математической модели объекта (1) может входить слагаемое с управлением:
при этом модель измерительной системы остается без изменений:
где вектор состояния, вектор возмущений, вектор управлений; вектор выхода (вектор измерений), вектор ошибок и погрешностей измерений, время, заданное положительное число. Заданы непрерывные матрицы , размеров соответственно.
Тогда структура наблюдателя состояния описывается уравнением
. (21)
При этом уравнение, описывающее изменение ошибки оценивания, не изменяется, и сохраняются формулы для нахождения .
Пример 1
Рассмотрим задачу синтеза наблюдателя в системе управления самолетом L-1011 [Chang J.-L, 2018], описываемой моделью нестационарной системы на конечном промежутке времени. В рассматриваемой задаче , , .
Тогда уравнение модели объекта управления (1) имеет вид
Уравнение измерительной системы (2):
где погрешности измерений описываются выражением:
Закон управления самолетом имеет вид [Chang J.-L, 2018]
где функция удовлетворяет дифференциальному уравнению
Уравнение для синтеза наблюдателя с учетом замечания 2 принимают форму
При решении задачи предлагается применить следующую методику.
- Найти матрицу решение дифференциального уравнения Риккати
2.Найти матрицу коэффициентов усиления наблюдателя
- Найти наихудшие законы изменения возмущения и погрешности измерений: .
- Оценить эффективность наблюдателя, исследуя динамику изменения ошибки наблюдения:
Для этого моделировать работу наблюдателя при ограниченных возмущениях и погрешностях измерений вида
где положительные числа.
Матрицы , и в (5) подбираются таким образом, чтобы обеспечивать корректный синтез наблюдателя в системе, а также желаемый вид переходных процессов в системе. Вид внешних воздействий и погрешностей измерения, а также подобранные матрицы, представлены в табл. 1.
Таблица 1
Параметры моделировани
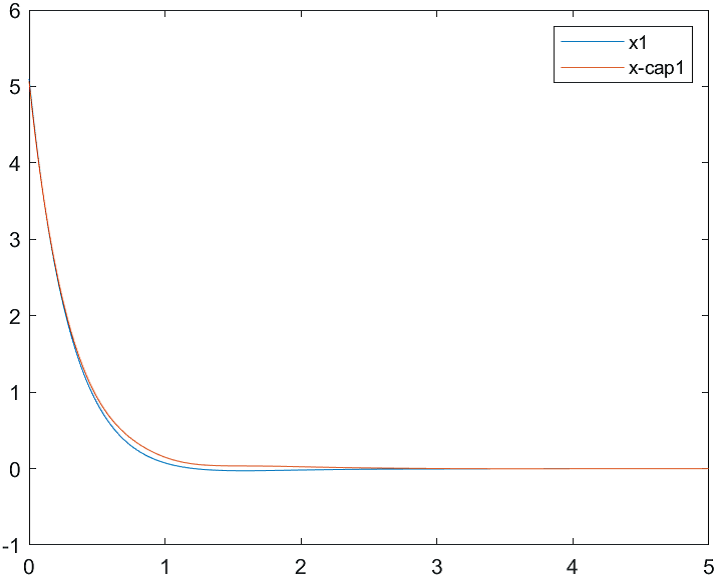
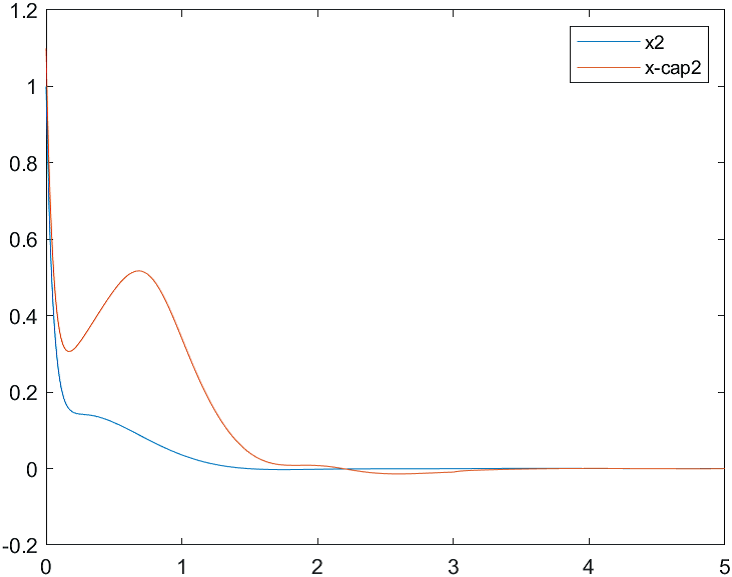
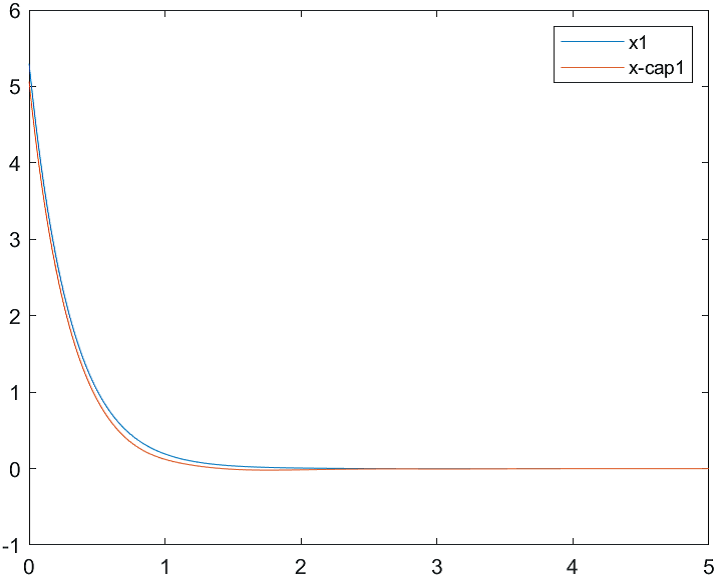
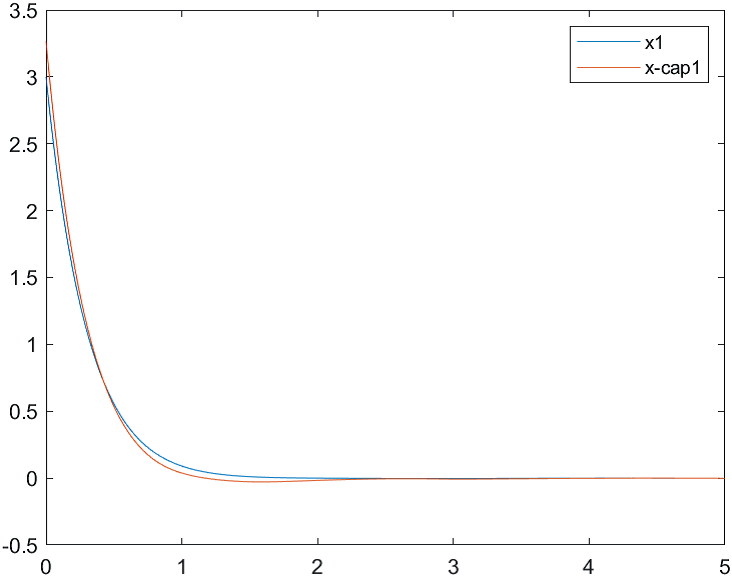
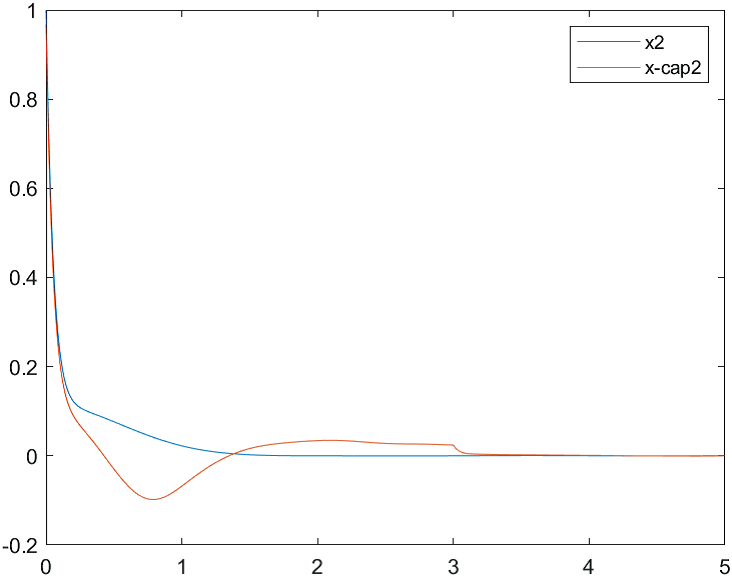
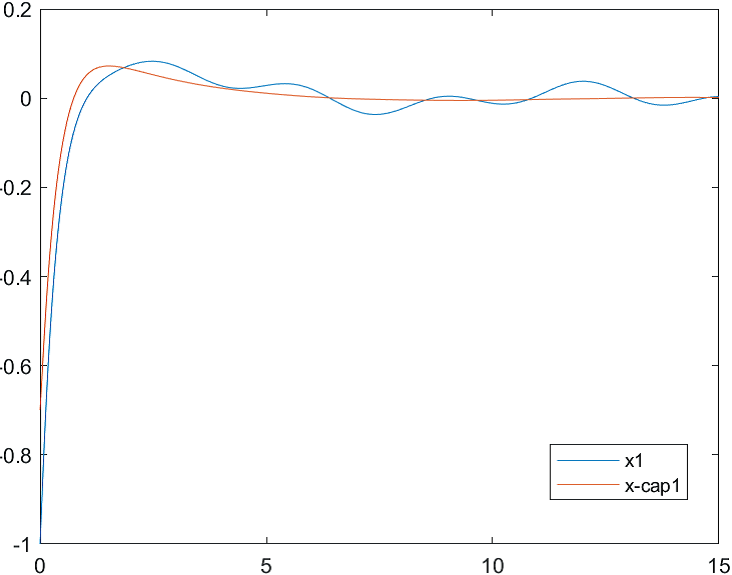
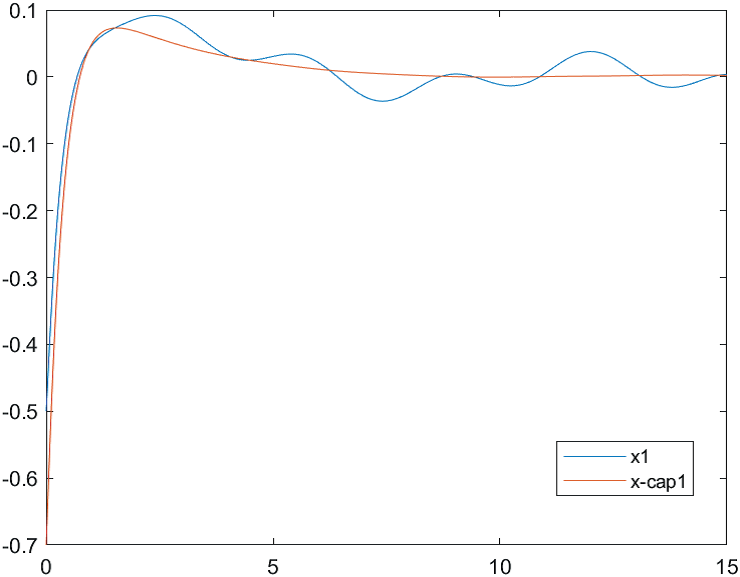
На рис. 1-3 отражены результаты моделирования системы управления совместно с наблюдателем состояния при различных начальных условиях:
а) , б) .
Начальные условия для оценки вектора состояния: .
|
Рис.1 Переходные процессы для координаты и ее оценки |
|
|
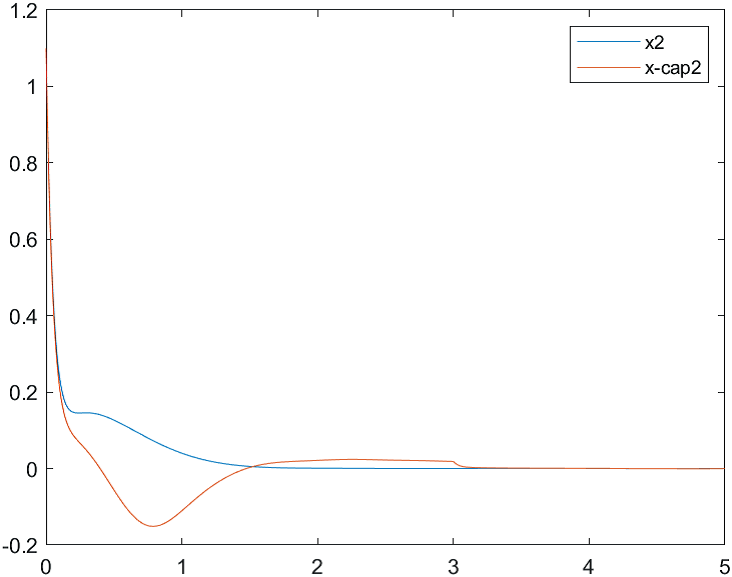
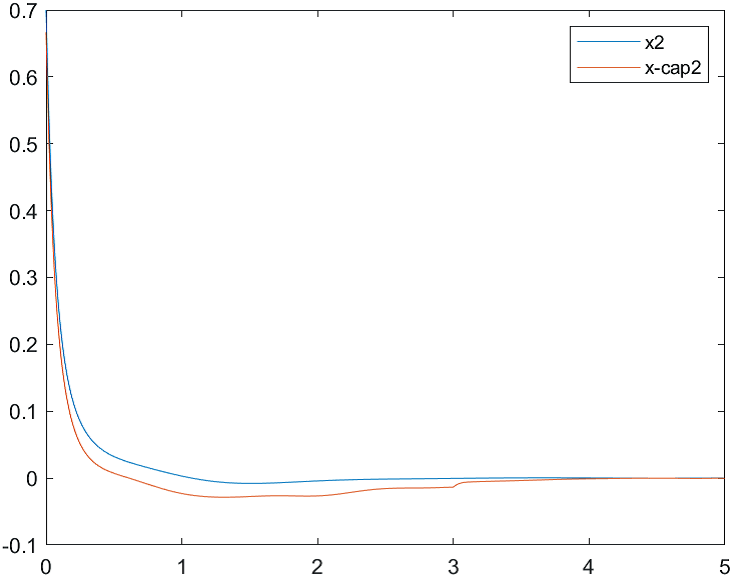
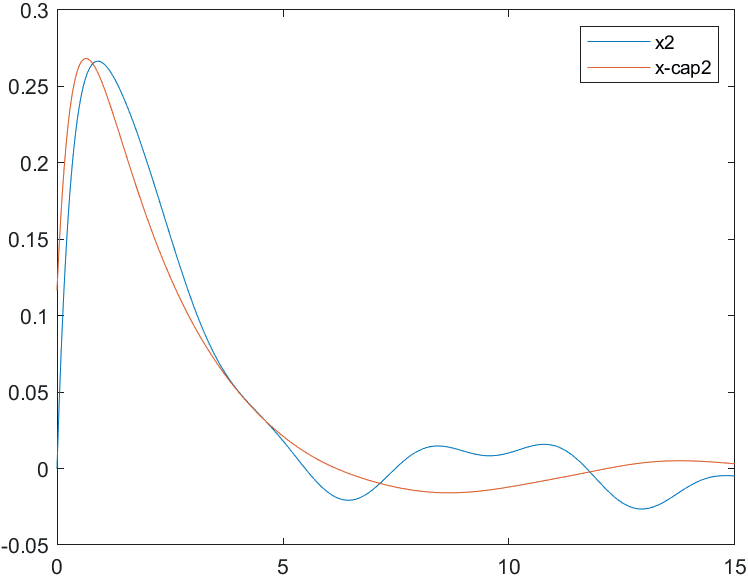
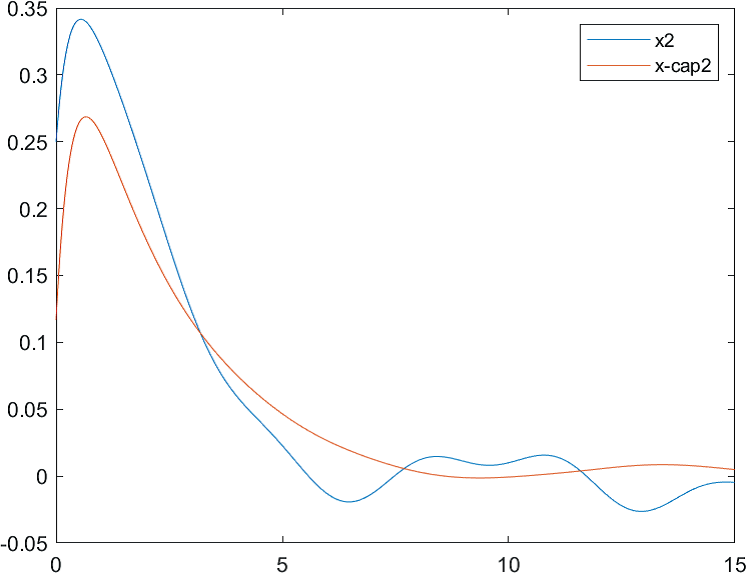
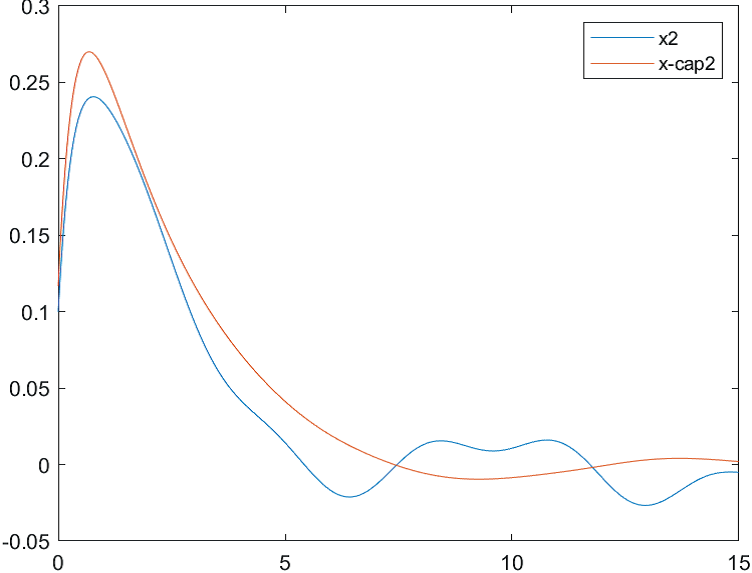
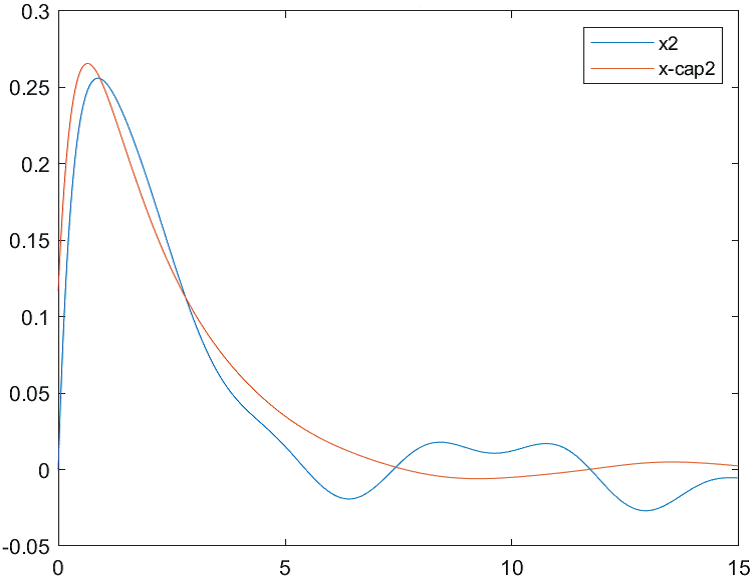
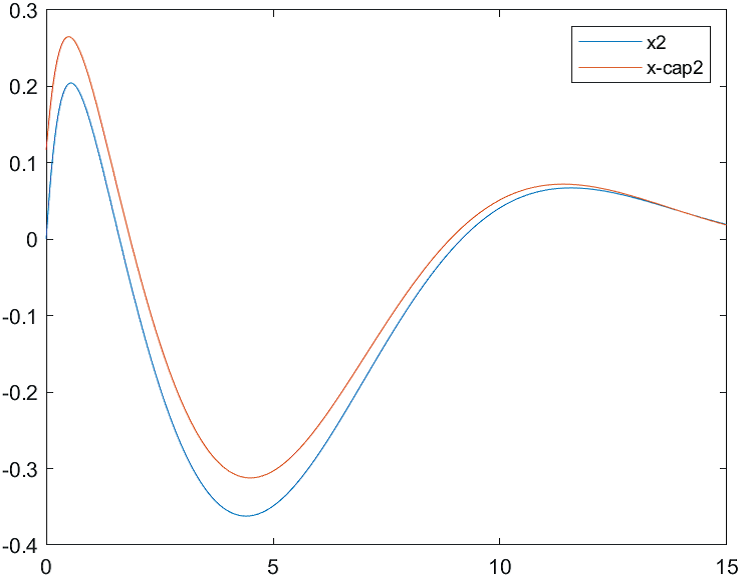
Рис.2 Переходные процессы для координаты и ее оценки |
|
|
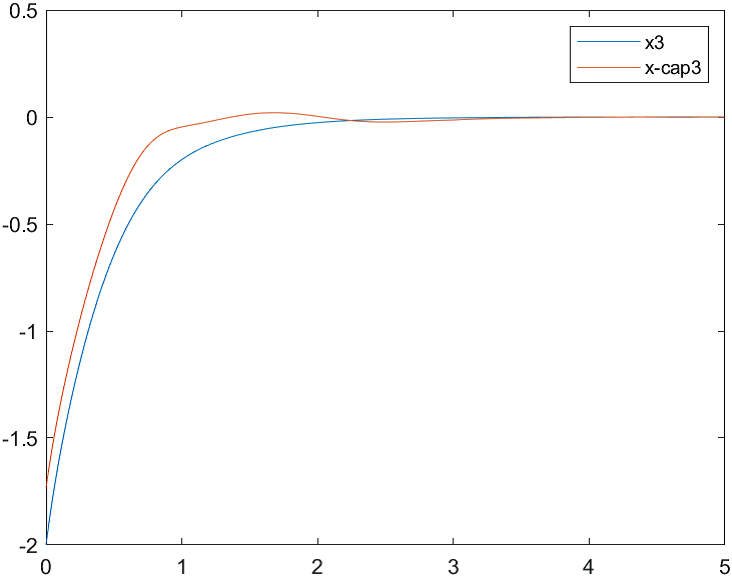
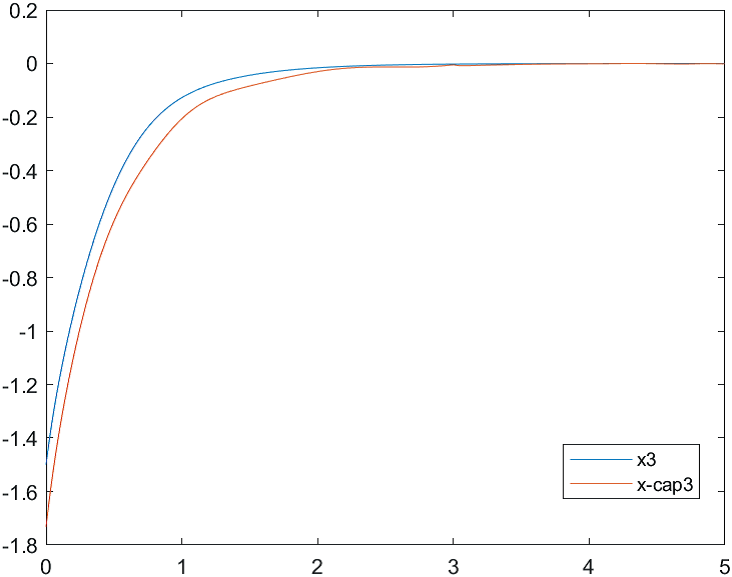
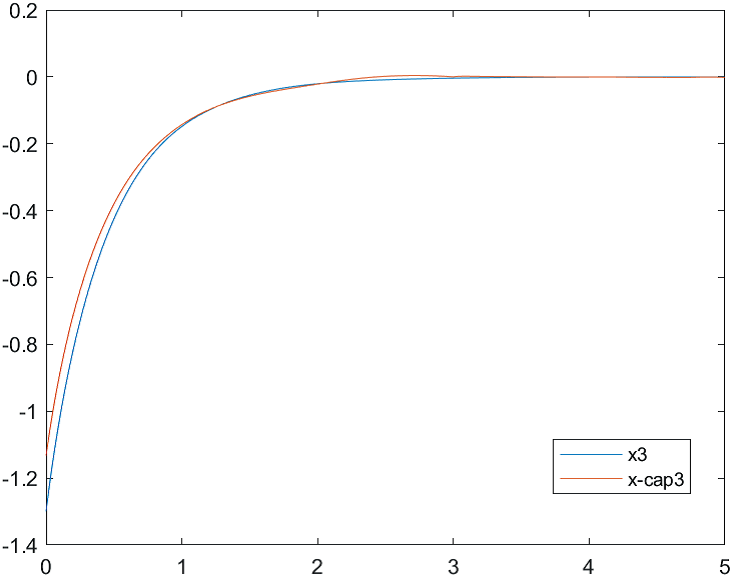
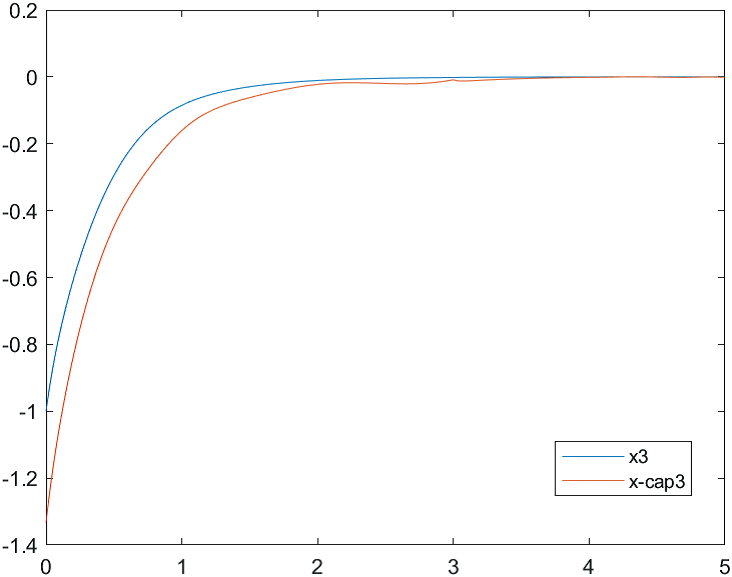
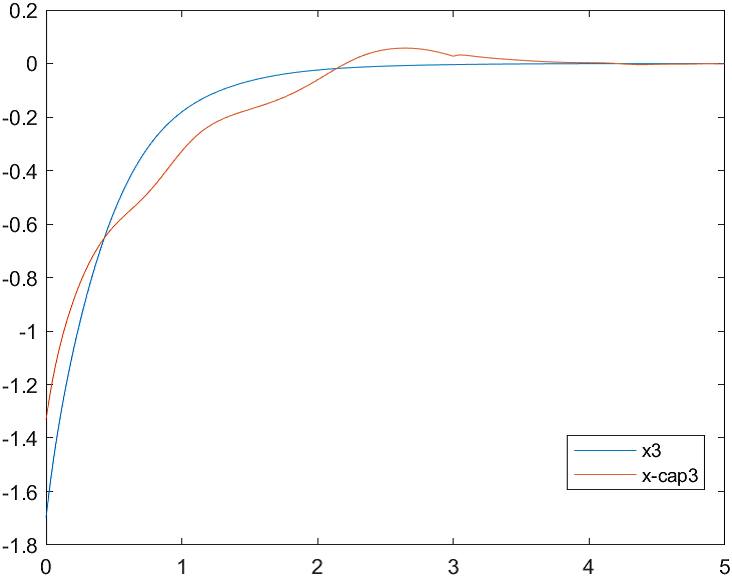
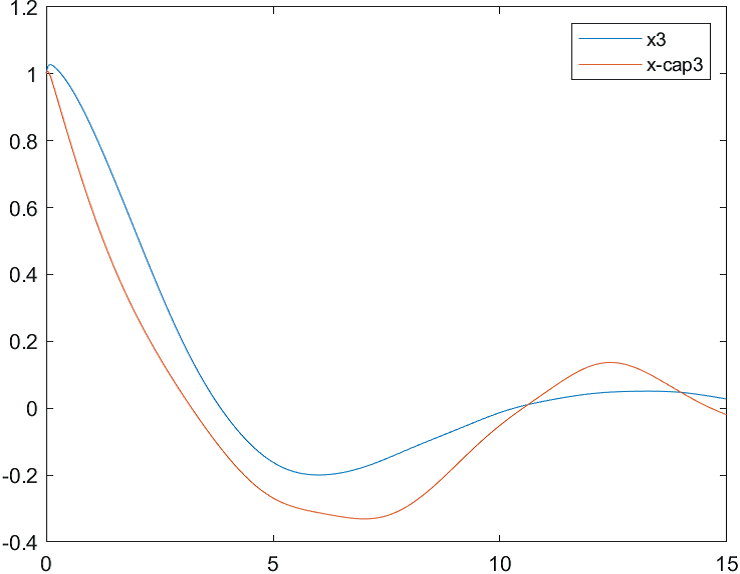
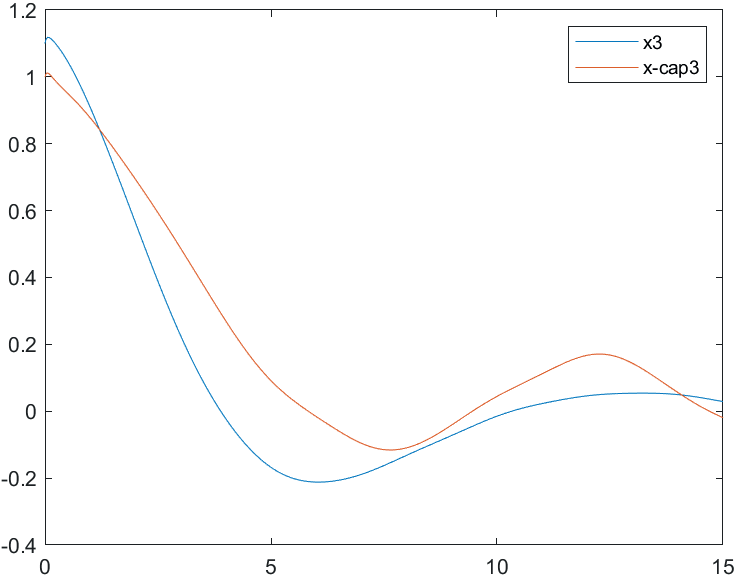
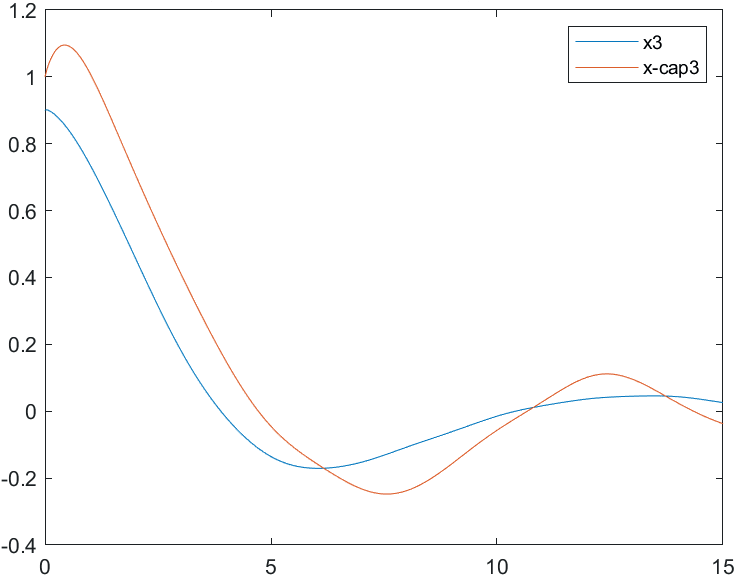
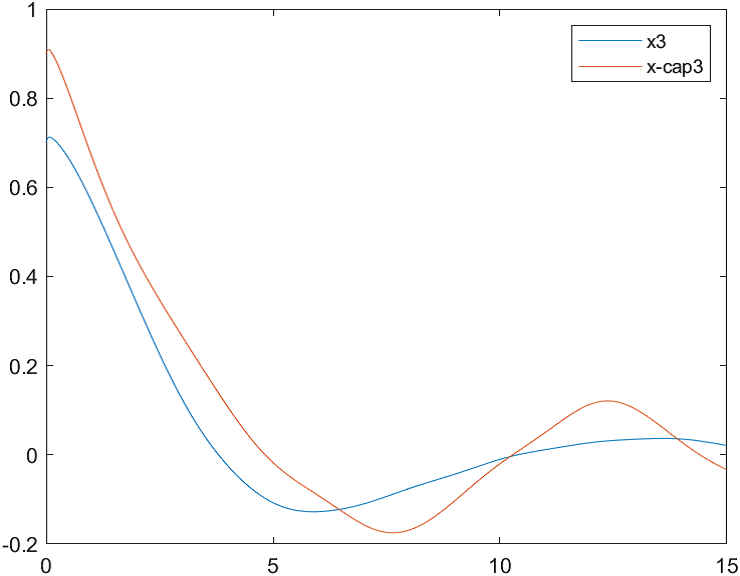
Рис.3 Переходные процессы для координаты и ее оценки |
|
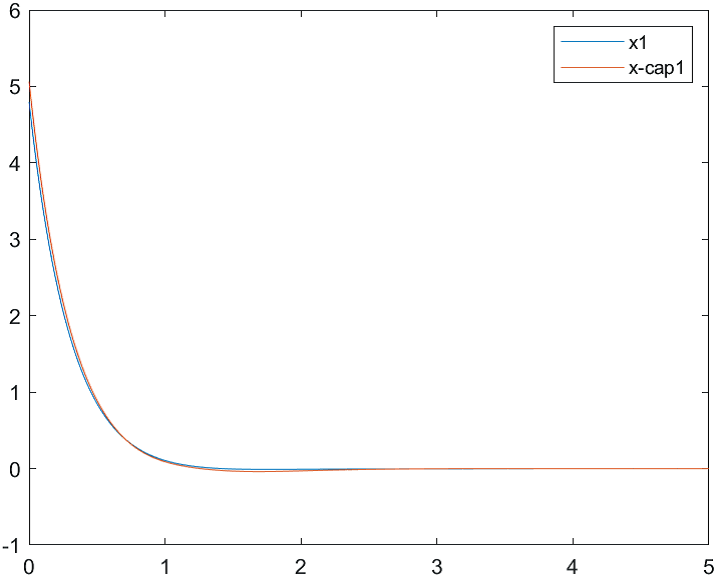
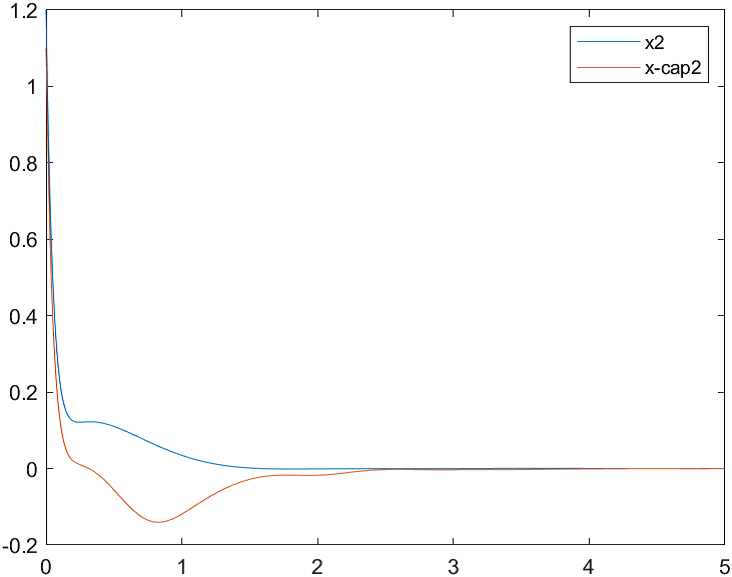
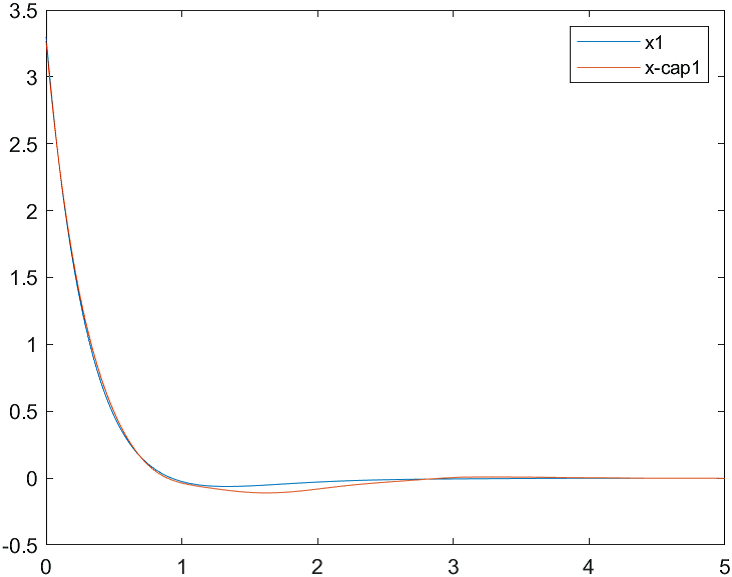
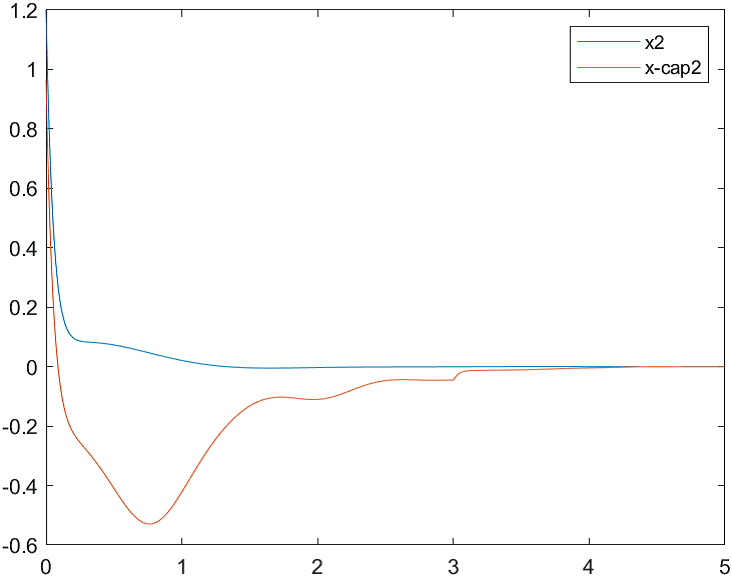
На рис. 4-6 представлены результаты моделирования системы с двумя различными начальными условиями для вектора состояния объекта и вектора его оценок:
а) , ;
б) , .
|
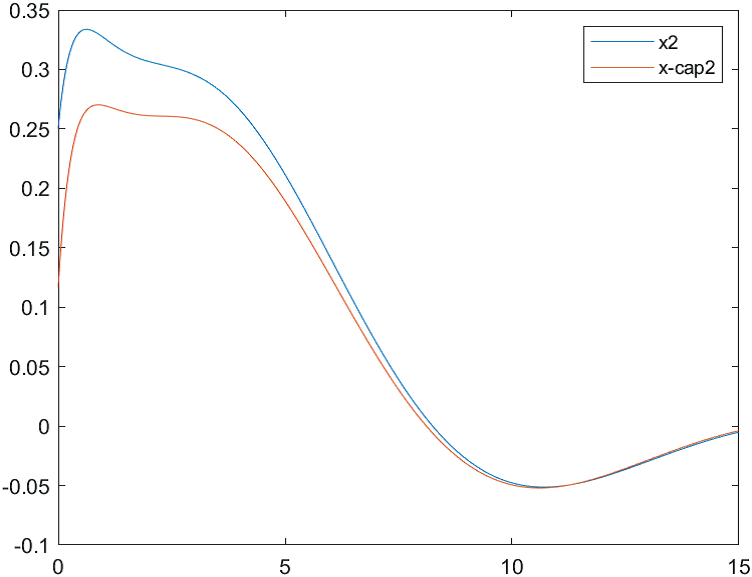
Рис.4 Переходные процессы для координаты и ее оценки |
|
|
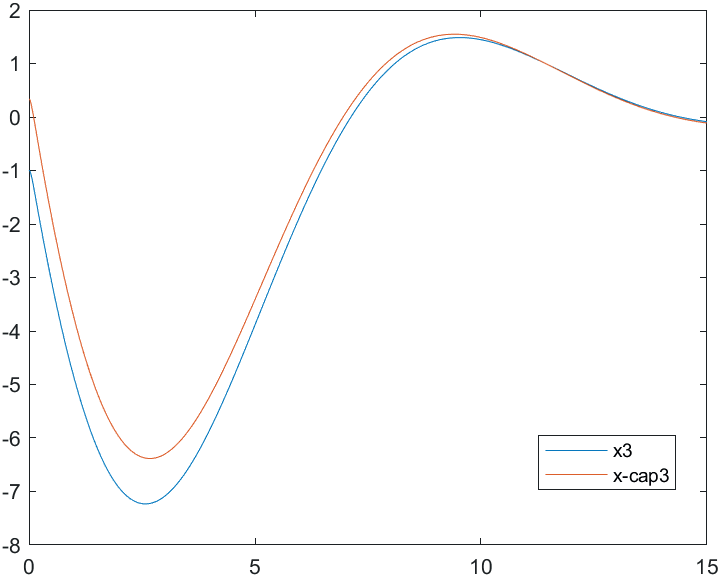
Рис.5 Переходные процессы для координаты и ее оценки |
|
|
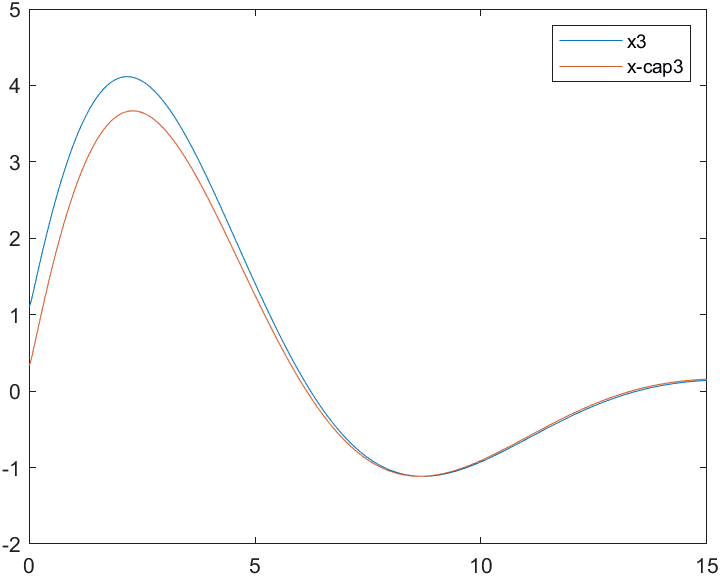
Рис.6 Переходные процессы для координаты и ее оценки |
|
На рис. 7-9 представлены результаты моделирования системы с двумя различными начальными условиями: а) , б) .
Начальные условия для оценки вектора состояния: .
|
Рис.7 Переходные процессы для координаты и ее оценки |
|
|
б) |
|
|
Рис.8 Переходные процессы для координаты и ее оценки |
|
|
Рис.9 Переходные процессы для координаты и ее оценки |
|
Анализ полученных результатов моделирования позволяет судить о стремлении ошибки оценивания к нулю при различных начальных условиях движения (при изменении параметра М переходные процессы аналогичны представленным).
Пример 2
Рассмотрим задачу синтеза наблюдателя в системе управления самолетом L-1011 [Chang J.-L, 2018], описываемой моделью стационарной системы на полубесконечном промежутке времени. В рассматриваемой задаче , , .
Тогда уравнение модели объекта управления (1) имеет вид.
Уравнение измерительной системы (2): .
Возмущение , а погрешность измерений:
Закон управления [Chang J.-L, 2018] имеет вид ,
где
При решении задачи предлагается применить следующую методику.
- Найти матрицу положительно определенное решение алгебраического уравнения Риккати
- Найти матрицу коэффициентов усиления наблюдателя
- Найти наихудшие законы изменения возмущения и погрешности измерений: , . (22)
- Оценить эффективность наблюдателя, исследуя динамику изменения ошибки наблюдения: , .
Для этого моделировать работу наблюдателя при ограниченных возмущениях и погрешностях измерений вида:
где положительные числа.
Матрицы , и в (5) подбираются таким образом, чтобы обеспечивать корректный синтез наблюдателя в системе, а также желаемый вид переходных процессов. Вид внешних воздействий и погрешностей измерения, а также подобранные матрицы, представлены в табл. 2.
Таблица 2
Параметры моделирования
На рис. 10-13 представлены результаты моделирования системы с различными начальными условиями: а) , б) .
Начальные условия для оценки вектора состояния: .
|
Рис.10 Переходные процессы для координаты и ее оценки |
|
|
б) |
|
|
Рис.11 Переходные процессы для координаты и ее оценки |
|
|
Рис.12 Переходные процессы для координаты и ее оценки |
|
|
Рис.13 Переходные процессы для координаты и ее оценки |
|
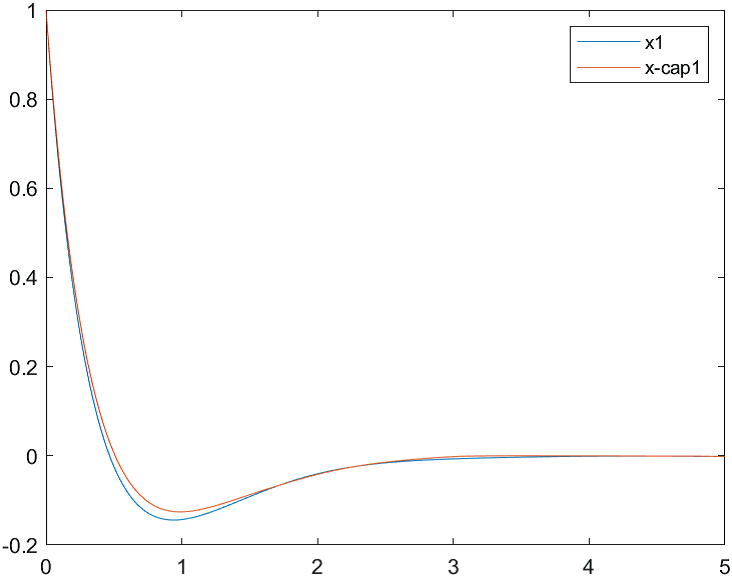
На рис. 14-17 представлены результаты моделирования системы с различными начальными условиями для вектора состояния и его оценки:
а)
б)
|
Рис.14 Переходные процессы для координаты и ее оценки |
|
|
Рис.15 Переходные процессы для координаты и ее оценки |
|
|
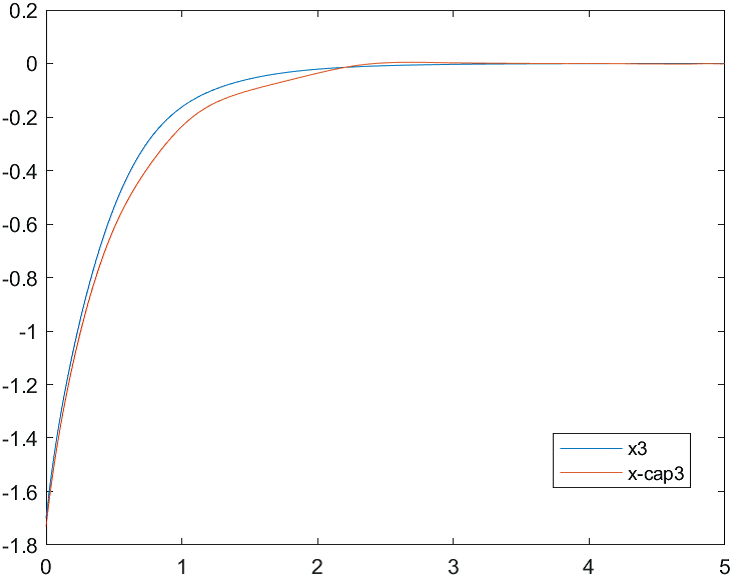
Рис.16 Переходные процессы для координаты и ее оценки |
|
|
Рис.17 Переходные процессы для координаты и ее оценки |
|
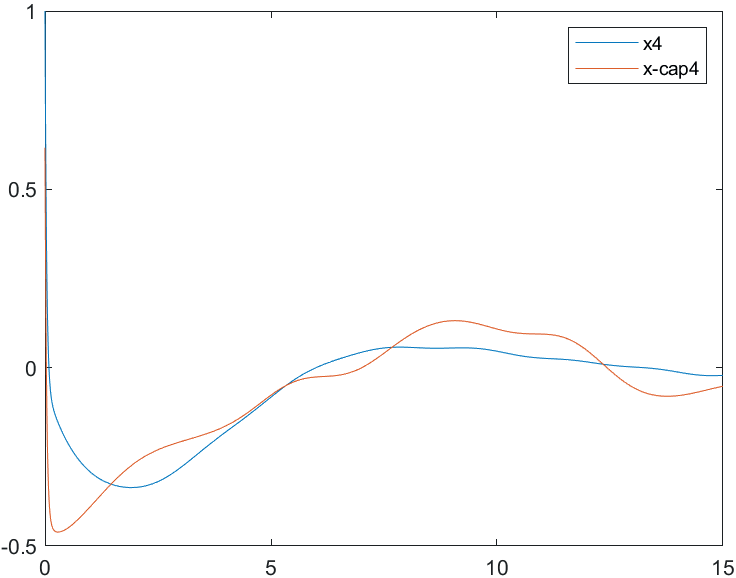
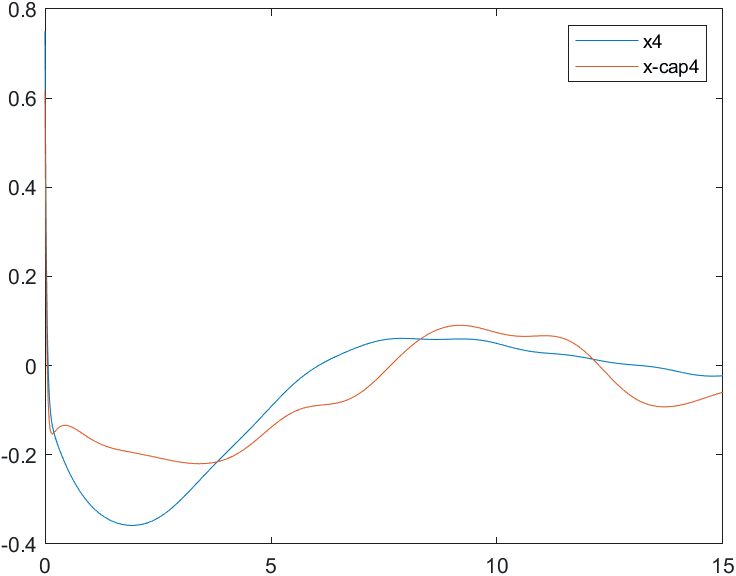
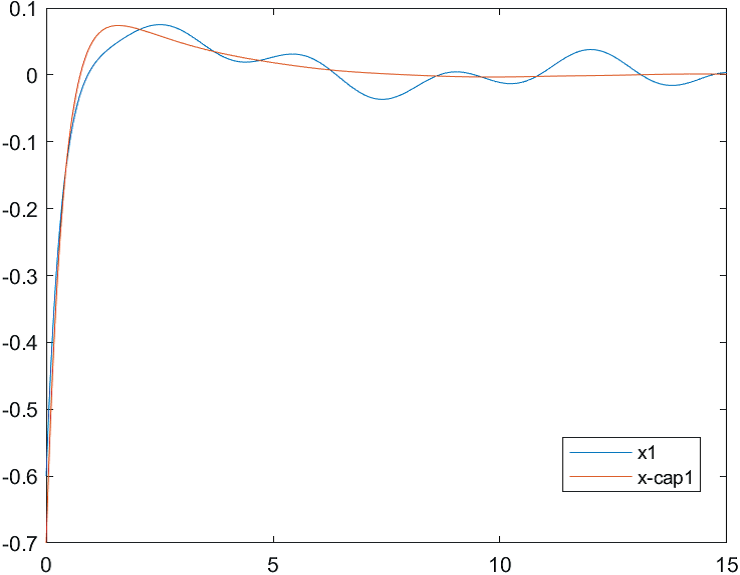
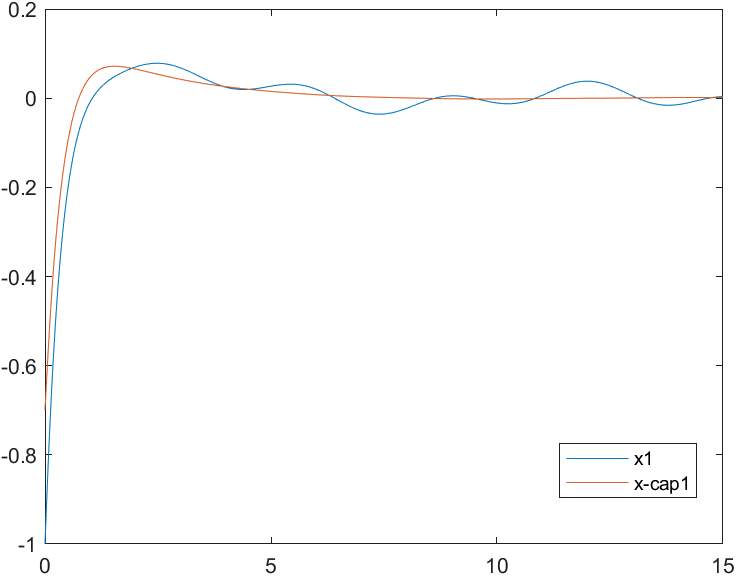
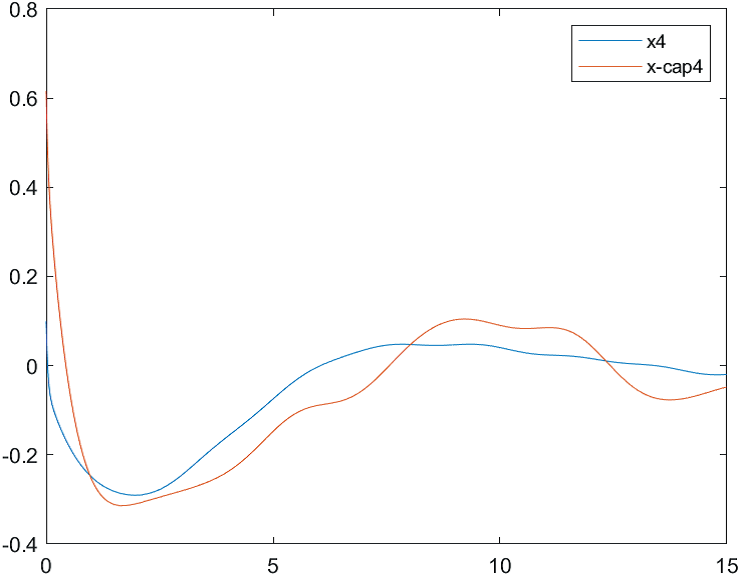
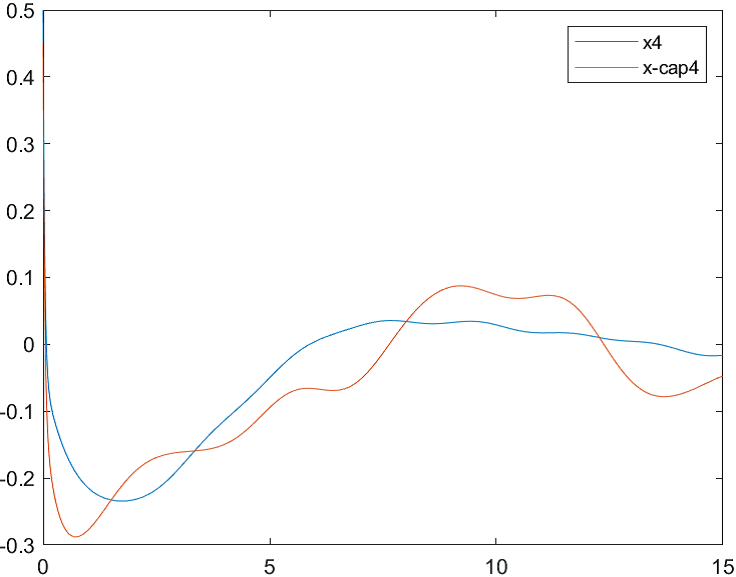
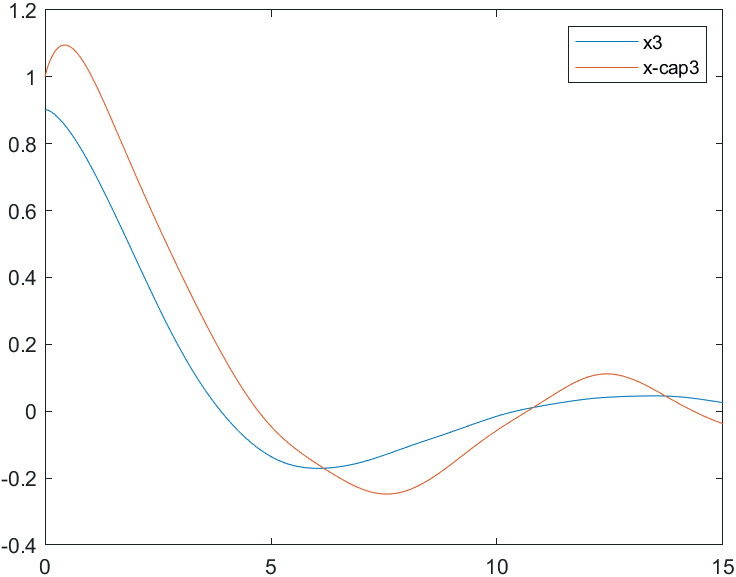
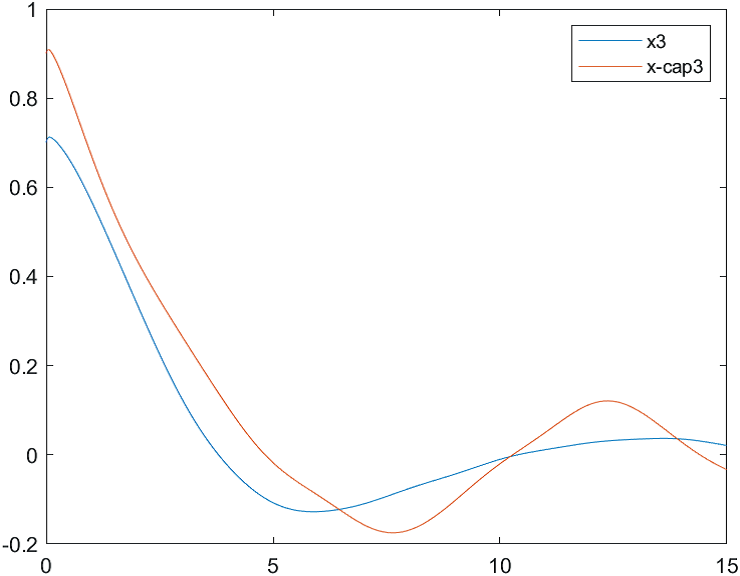
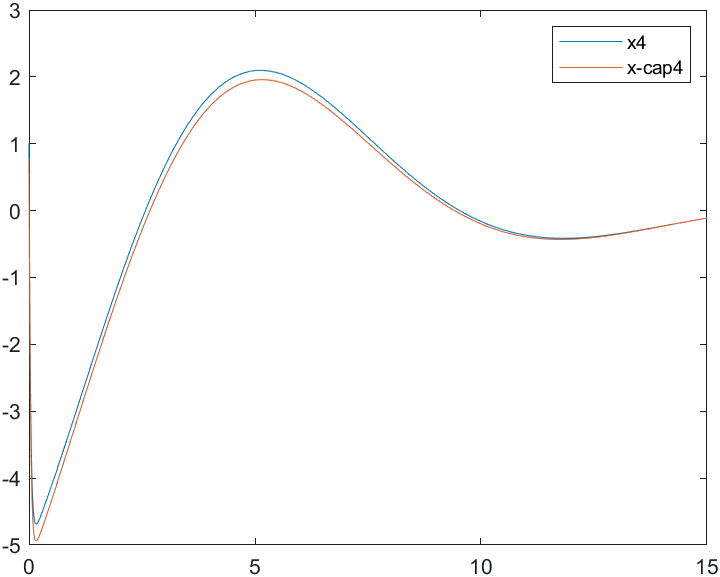
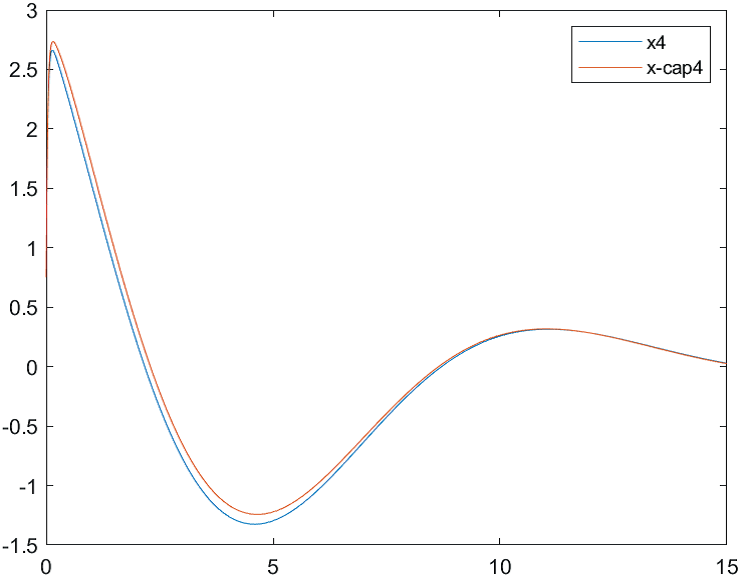
На рис. 18-21 представлены результаты моделирования системы при воздействии на систему наихудших возмущений и погрешностей измерений (22). Начальные условия для вектора состояния объекта и оценки вектора состояния:
а)
б)
|
Рис.18 Переходные процессы для координаты и ее оценки |
|
|
Рис.19 Переходные процессы для координаты и ее оценки |
|
|
Рис.20 Переходные процессы для координаты и ее оценки |
|
|
а) |
|
|
Рис.21 Переходные процессы для координаты и ее оценки |
|
На основании рис. 10-21 можно сделать вывод, что предложенный подход к синтезу наблюдателя системы позволяет получить достаточно точную оценку координат вектора состояния и желаемое качество переходных процессов в условиях неполной информации о состоянии объекта, ограниченных начальных условиях, внешних воздействиях и погрешностях измерений.
Для произведения вычислений и моделирования использовалась система компьютерной математики MATLAB.
Заключение
В статье сформулированы и на основе принципа расширения доказаны достаточные условия существования наблюдателя. Получены соотношения для нахождения параметров наблюдателя и наихудших законов изменения внешних воздействий и погрешностей измерений. Решены две прикладные задачи оценивания вектора состояния самолета по результатам неполных и неточных измерений. На основании полученных результатов можно сделать вывод, что предложенный подход к синтезу наблюдателя позволяет получить достаточно точную оценку вектора состояния, обеспечивает желаемое качество переходных процессов и обеспечить асимптотическую устойчивость системы в условиях неполной информации. Предложенный метод оценивания вектора состояния может быть применен к различным задачам управления, например, при проектировании автопилотов или систем автоматической навигации летательных аппаратов.