Использование образов в преподавании высшей математики

Куланин Е.Д.; Степанов М.Е.

doi:10.17759/mda.2024140213

Моделирование и анализ данных
2024. Том 14. № 2. С. 192–225
doi:10.17759/mda.2024140213
ISSN: 2219-3758 / 2311-9454 (online)

Использование образов в преподавании высшей математики

0

Куланин Е.Д., Степанов М.Е.

Аннотация

Статья продолжает цикл методических разработок авторов [1] – [17]. В ней обсуждаются некоторые проблемы, связанные с путями повышения культуры математического мышления студентов-математиков. Авторы опираются на опыт работы на факультете информационных технологий МГППУ.

Общая информация

Ключевые слова: высшее образование, методика преподавания математики, аналитическая геометрия, математический анализ

Рубрика издания: Методика преподавания

Тип материала: научная статья

DOI: https://doi.org/10.17759/mda.2024140213

Получена: 22.01.2024

Принята в печать: 06.03.2024

Для цитаты: Куланин Е.Д., Степанов М.Е. Использование образов в преподавании высшей математики // Моделирование и анализ данных. 2024. Том 14. № 2. С. 192–225. DOI: 10.17759/mda.2024140213

Полный текст

ВВЕДЕНИЕ

Любая область человеческой деятельности в той или иной мере становится полем противоборства, как отдельных специалистов, так и коллективов, работающих в данной сфере. Наука вообще и математика в частности не являются исключениями.

Причин для этого очень много. В частности, значительную роль играют меркантильные интересы, связанные со стремлением к материальному благополучию, славе и так далее. Обсуждать подобные мотивы внутренней нестабильности в науке мы, естественно, не будем. Напомним только слова Томаса Гоббса из «Левиафана», переиначенные потом В. И. Лениным: «Я не сомневаюсь, что если истина, что сумма углов треугольника равна сумме двух углов квадрата, противоречила бы чьему-либо праву на власть или интересам тех, кто уже обладает властью, то, поскольку это было бы во власти тех, чьи интересы задеты этой истиной, учение геометрии было бы если не оспариваемо, то путем сожжения книг по геометрии было бы вытеснено».

Несомненно, существуют и иные, в известном смысле объективные, причины жарких научных споров. Они проистекают из того обстоятельства, что наука постоянно развивается и развивается непредсказуемо. Само собой, что разные учёные и различные научные школы неизбежно имеют различные точки зрения на протекающие в научной сфере процессы. Ну, а разные парадигмы по-разному формируют представление о выборе подходов к развитию научного направления. Упомянем о споре между В. И. Арнольдом и Ю. И. Маниным.

Выдающийся математик В. И. Арнольд неоднократно подчеркивал, что в мировой науке существует так называемая «мафия левополушарных математиков», исключающих из образования развитие пространственно-математического мышления. Напомним, что левое полушарие мозга отвечает за речь и формальную логику, а правое – за образное мышление и интуицию. Вся содержательная сущность математики левополушарными математиками подменяется манипуляциями, которые нет смысла применять ни в какой другой науке из-за полной их бесполезности. Другой выдающийся математик Ю. И. Манин в дискуссии с В. И. Арнольдом откровенно признался, для чего это делается: основная задача постмодернистской математики вовсе «не в том, чтобы, как думают некоторые, ускорять прогресс человечества, а в том, чтобы этот прогресс всемерно тормозить».

Иначе говоря, интеллектуальные силы лучших математиков преднамеренно бросаются на бесцельные «игры разума». Причем это делается сознательно, на высшем уровне управления человеческой цивилизацией, чтобы математику не использовали для осмысления окружающей действительности и тех рукотворных кризисов, с помощью которых удается «цивилизованно» порабощать целые народы.

Пока речь шла о тонкой прослойке математиков-исследователей, но левополушарные математики сумели активно повлиять на изучение математики. Им удалось затронуть не только высшую школу, но они добрались и до школьного образования. Вместо освоения счёта в начальной школе стали изучать формулировки абстрактных алгебраических законов, описывающих коммутативность, ассоциативность, дистрибутивность. Для тех, кто не умеет считать, знание этих законов не только бесполезно, но и вредно.

Одним из экстремистов левополушарного толка был Жан Дьедонне, один из основателей группы «Бурбаки». Введение к его учебнику [18] можно рассматривать как воинствующий манифест, направленный на изгнание геометрических образов из математического образования и замену их крайне абстрактными логическими схемами. Точка зрения Дьедонне в целом понятна и обоснована достаточно подробно. Он утверждает, что каждый исторический выход математики на новый уровень развития заставляет переосмыслить даже известные с древнейших времён математические понятия по-новому. В частности, это относится к геометрическим объектам, испокон веков изучаемым в рамках евклидовой геометрии. Для Дьедонне эта форма геометрического знания не только архаична, но и вредна.

Дьедонне отрицает необходимость изучения целого ряда традиционных разделов как элементарной, так и высшей математики, в том числе тригонометрию, аналитическую, проективную, неевклидову геометрии и даже теорию комплексных чисел. Впрочем, он признаёт, что специалистам в некоторых областях науки и техники тригонометрия нужна. Речь идёт об астрономах, геодезистах и авторах учебников по тригонометрии.

Вот что он пишет о том, чем следует заменить традиционные дисциплины: «Отправляясь от очень простых аксиом – в отличие от сложных аксиом Евклида – Гильберта, – можно при помощи тривиальных вычислений непосредственно и в несколько строчек получить всё то, для чего раньше нужно было возводить леса искусственных и сложных систем треугольников, чтобы во чтобы во чтобы ни стало свести задачу к священным случаям «равенства» и «подобия» треугольников – к единственной основе всей традиционной технике Евклида». Таким образом, Дьедонне предполагает, что преподавание математики может производиться по аналогии с изложением той или иной математической дисциплины на основе логического вывода теорем из аксиом и доказанных ранее теорем. Такой подход является в высшей степени формальным.

Прежде всего, здесь можно отметить полный отрыв от реалий окружающего мира, то есть от численных отношений и пространственных форм окружающего нас мира (А. Н. Колмогоров). Допущение о возможности обучения чисто логическим путём является абсолютно неверным. Хотя вряд ли это обстоятельство могло обеспокоить Дьедонне. Достаточно обратиться к одному из его замечаний по поводу построения школьного курса математики: «… могу высказать только некоторые «вольные мысли» ввиду моей полной некомпетентности в вопросах реакций детей возраста 11 – 14 лет». Этого признания вполне достаточно, чтобы не вмешиваться в решение педагогических вопросов, однако, Дьедонне агрессивно навязывает свою «методу». При этом он подчёркивает, что она должна быть введена при обучении всех детей поголовно и во все средние школы.

Обсуждение взглядов французского математика может показаться не слишком актуальным, но дело в том, что во всём мире были подвергнуты реформированию программы, направленные на изучение математики не только в средней, но и начальной школе. С первого класса, были навязаны термины теории множеств и изгнаны счётные палочки и счёты. Цель – воспитание абстрактно мыслящих людей. Результат – понижение интеллектуального уровня выпускников школы, а, в конечном счёте, и всего человечества.

Человек осваивает логику стихийно, опираясь на всю полноту взаимодействий с окружающим миром. В своей книге «Наука логики» [19] великий немецкий философ Георг Вильгельм Фридрих Гегель писал, что логика сама по себе не учит мыслить. Мыслит человек, поскольку это является его сущностью. Точно так же он прекрасно может переваривать пищу, не зная анатомии и физиологии. Из этого следует, что логика является всего лишь одним из инструментов познания. Она, конечно, очень важна, но, в конечном счёте, она может работать только в сочетании с образным мышлением. Вообще же левое и правое полушария мозга должны сотрудничать, а не противоборствовать.

Кроме того, полезно вспомнить то, что Алексей Фёдорович Лосев говорит в своей работе [20] о восприятии бытия в его перспективности и рельефности. По его мнению, именно такое восприятие создаёт полноту личности. А, по мнению авторов статьи, перспективное и рельефное восприятие мира связано именно с образным мышлением. По мере сил они пытаются разрабатывать методические приёмы, относящиеся к преподаванию сложных математических вопросов из самых разных областей математики.

Авторы статьи – рядовые преподаватели, а Жан Дьедонне был крупным математиком. Имеют ли авторы право критиковать столь заметную персону? Ответ прост. Специалист любого уровня имеет право на своё мнение. К тому же быть видным математиком, не значит хоть что-то понимать в педагогике.

Кроме того, одним из результатов педагогических усилий группы Бурбаки стал упадок математики. Этот факт ярко комментирован В. И. Арнольдом [21]. Приведём соответствующую цитату.

«Абстрактное» гладкое многообразие — это гладкое подмногообразие какого-либо евклидова пространства, рассматриваемое с точностью до диффеоморфизма. Никаких «более абстрактных» конечномерных гладких многообразий в природе не существует (теорема Уитни). Зачем же мы до сих пор мучаем студентов абстрактным определением? Не лучше ли доказать им теорему о явной классификации двумерных замкнутых многообразий (поверхностей)?

Именно эта замечательная теорема (утверждающая, например, что всякая компактная связная ориентируемая поверхность — это сфера с некоторым числом ручек) даёт правильное представление о том, что такое современная математика, а вовсе не сверхабстрактные обобщения наивных подмногообразий евклидова пространства, не дающие на самом деле ничего нового и выдаваемые аксиоматизаторами за достижения».

Это мнение достаточно весомо и указывает на крайнюю ущербность педагогических установок Дьедонне. Тем не менее, определённая группа математиков может быть убеждена в правильности соответствующего подхода. Тем более, что основным обоснованием здесь является необходимость обновления математического образования. И, конечно, обновление необходимо. Вопрос только в том, в какой форме его проводить.

Естественно, что путей обновления может быть предложено достаточно много. В результате возможно активное противоборство между сторонниками различных подходов. Это противоборство может перерасти в войну. И победит сильнейший. Так, например, и произошло с победой установок Дьедонне. Сила аксиоматизаторов в поддержке, которую оказывают им сильные мира сего. Причины этой поддержки в стремлении мировых элит понизить интеллектуальный уровень населения земного шара.

Правильный путь обновления системы образования состоит не в том, чтобы огульно внедрить чьи-то прожекты, а в проведении долговременных педагогических экспериментов, позволяющих сравнить традиционные и инновационные методики. И в первую очередь проверяться должны те планы обновления образования, которые требуют обновлять всё без изъятия и повсеместно. Скрупулёзная проверка – это долгий путь, но наиболее безопасный для общества.

Что касается методических разработок частного характера, которые делают рядовые преподаватели для своих нужд, то они не затрагивают систему образования в целом, а, значит, не могут принести особого вреда даже в тех случаях, когда они заведомо неудачны. В этом случае их просто можно подвергнуть аргументированной критике. Те соображения, которые высказывают авторы данной статьи, как раз и относятся к этому виду методических разработок.

Однако в ряде случаев преподавателям удаётся прийти к удачным идеям, которые могут стать эффективными инструментами в преподавании математики. В любой работе, тем более сложной, нужны различные инструменты. Ими можно пользоваться не всегда, а именно тогда, когда это целесообразно.

В данной статье авторы предлагают несколько скромных методических разработок, основанных на использовании образов математического характера. Авторы хотят ими поделиться, чтобы по мере надобности их могли использовать преподаватели, а в ряде случаев и студенты.

Итак, далее будет описана совокупность различных методических приёмов, объединённых интуитивно-образным подходом. Авторы ни в коем случае не претендуют на новизну. Некоторые из этих приёмов имеют многовековую историю, но их нельзя забывать, особенно после целенаправленной атаки на них со стороны формалистов-реформаторов. Всё, что позволяет студенту понять математику, должно быть включено в рабочий инструментарий каждого преподавателя.

ПОНЯТИЕ ФУНКЦИИ

Возникновение новой математики, во многом начатое Рене Декартом, было направлено на разработку математических понятий, связанных с описанием механического движения. По этой причине многие понятия математического анализа, которые постепенно были формализованы, например, с помощью эпсилон-дельта языка, становятся понятными только при динамической интерпретации. Например, понятие предела глубинно связано с представлением о затухающем маятнике. Смысл затухания колебаний в том, что с некоторого момента времени отклонение маятника от положения равновесия становится сколь угодно малым.

Центральным понятием математического анализа является функция, рассматриваемая как взаимосвязь значений двух переменных. Что касается переменных, то их можно интерпретировать как свойства различных объектов и явлений, выражаемые с помощью чисел. Физический смысл переменных может быть весьма разнообразным, но при изучении функций наиболее важными являются два.

Аргумент функции интерпретируется как время, а значения функции – как пройденный путь.
Аргументы и значения функции интерпретируются как координаты декартовой плоскости.

В качестве числовых значений переменных величин в классическом анализе рассматриваются действительные числа. Они могут на выбор рассматриваться как сечения в поле рациональных чисел, как десятичные дроби и как точки евклидовой прямой. Связь этих точек зрения устанавливается с помощью процедуры измерения отрезков.

Множество действительных чисел в целом следует представлять себе как геометрический или точнее топологический образ – континуум. Именно по этой причине в математическом анализе неразрывны аналитический и геометрический подходы.

Таким образом, идеи математического анализа изначально пронизаны как геометрическими и кинематическими образами, так и представлениями, связанными с числами и вычислительными процедурами, достигающими своего максимального развития в исчислениях различного вида. Образ непрерывной линии (континуума, прямой, кривой, нити, стержня и т. д.) является исходным образом для уяснения геометрического и кинематического истолкования понятия функции. С физической же точки зрения функцию следует рассматривать как теоретическую модель процесса. Не менее важный путь к аналитическому истолкованию понятия функции связан с арифметическим и алгебраическим понятием последовательности. Все эти представления, видимо, можно считать архетипическими для человеческой психики. Именно отправляясь от них, следует формировать научное представление о функции.

Сделаем два замечания. Прежде всего, кому-то может показаться, что определение функции как отображения вполне достаточно для дальнейшего свободного использования этого понятия. Авторы считают, что необходимо всестороннее и детальное рассмотрение понятия функции. К этому вопросу мы вернёмся далее.

Второе замечание связано с тем, что исходные архетипические образы человеческой психики являются базой для освоения научных понятий. Но процесс обучения как раз и состоит в том, что по его ходу осуществляется развитие исходного образа (или образов), его усложнение и логическое освоение.

Перейдём к вопросу о всестороннем рассмотрении понятия функции на младших курсах в высшей школе. Прежде всего, отметим, что простейшие виды функций рассматриваются уже в школьном курсе математики. Это, однако, не гарантирует того, что студент, приступая к изучению математического анализа, достаточно ясно представляет себе, чем является функция как таковая.

Чтобы достичь достаточно глубокого понимания, необходимо выйти за рамки абстрактного теоретико-множественного описания функции и соединить воедино кинематическое истолкование этого понятия, геометрический образ функции (график) и аналитическое её описание, часто восходящее к рассмотрению числовой последовательности определённого вида. Связь функций и числовых последовательностей, кстати, проявляется в важнейшем для инженерных приложений табличном представлении функций. При этом с табулированием функций связаны и важные теоретические проблемы математики [22].

В статье [14] рассматриваются некоторые вопросы, связанные с образным описанием переменных и функций. Приведём несколько цитат, в которых кратко формулируются некоторые положения, позволяющие прийти к образам переменных и функций с акцентом на физические и геометрические аспекты соответствующих понятий.

Цитата 1: «Определение понятия переменной величины как свойства объекта, выраженного действительным числом. Спиртовой термометр как модель переменной величины. Геометрическая модель переменной величины – числовая прямая, по которой движется точка-указатель. Функция y = f(x) как зависимость между двумя переменными. Примечание: обычно понятие переменной сводится к процедуре произвольного выбора значений из определённого множества. При этом, хотя бы отчасти, теряется физический смысл понятия «переменная». Этот смысл состоит в том, что переменная даёт числовое выражение некоторых свойств объектов окружающего мира. Именно для этого переменные и нужны. В рамках классической математики переменные также выражают свойства объектов, например, в геометрии речь идёт о длинах, площадях, объёмах и т. д. В свою очередь, признав, что переменная является выразителем свойств, следует беспорядочный «выбор значений» заменить «изменением», то есть движением указателя вдоль числовой прямой. Именно такое интуитивное представление соответствует физическому смыслу термина «переменная». Хотя с точки зрения логики и возможности обобщений именно «выбору значений» может быть отдано предпочтение».

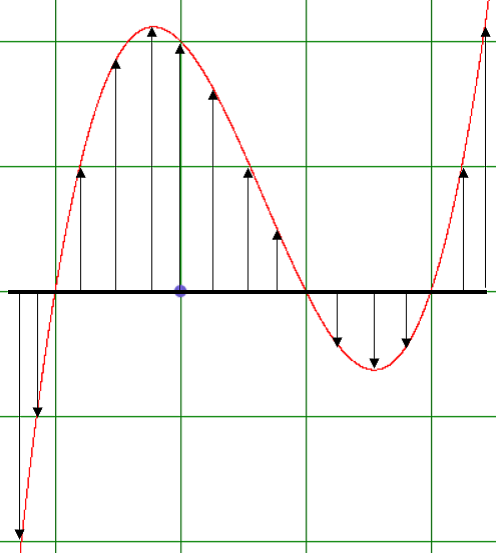
Цитата 2: «Пластический образ континуума. Целью данного пункта является наглядное объяснение причин, по которым график функции является кривой. Само объяснение таково. Представим себе, что на оси абсцисс в декартовой плоскости расположен пластичный, легко деформируемый стержень. Ординаты всех его точек равны нулю. Стержень можно параллельно оси абсцисс переместить вверх или вниз на некоторую величину с. При этом ординаты всех его точек примут одинаковые значения с, уже неравные нулю. С помощью этой процедуры построен график функции у = с. Пусть далее нам дана функция y = f(x). Теперь мы будем перемещать по вертикали не весь стержень целиком, а каждую его точку х сдвинем на своё особое расстояние y = f(x). При этом стержень деформируется. Он даже может разорваться, но если для близких значений абсцисс, значения ординат тоже близки, то разрывов не будет, а график функции предстанет в виде кривой».

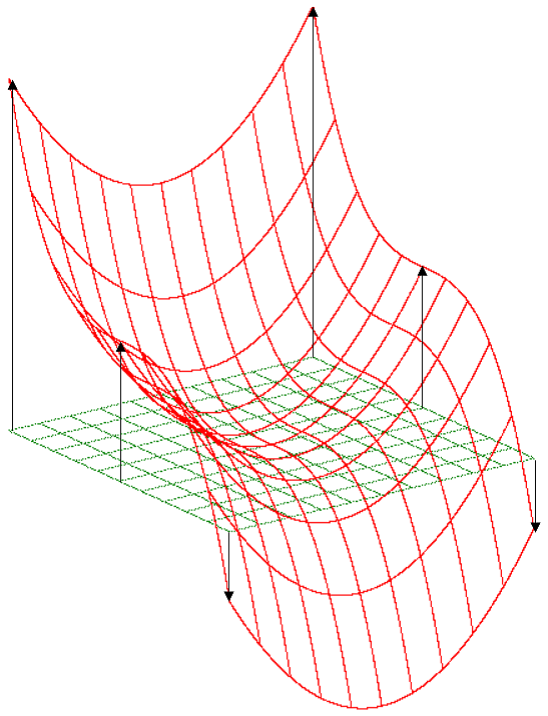
Цитата 3: «Пластический образ поверхности как аналога графика функции двух переменных. Представим себе, что на декартовой плоскости расположен пластичный, легко деформируемый ковёр. Каждая точка ковра определяется парой координат (х; у). Если же нам дана функция от двух переменных z = f(x, y), мы каждую точку ковра (х; у) сдвинем по вертикали (уже в трёхмерном пространстве) на своё особое расстояние z = f(x, y). При этом ковёр деформируется и превратится в аналог графика функции от двух переменных, а именно в некоторую поверхность».

Итак, смысл понятия «переменная» связан с изменением. Функция, как описание взаимосвязи двух изменяющихся переменных, представляет собой абстрактную модель какого-либо процесса. Геометрический образ функции связан с представлением о пластичном стержне. После его преобразования в график функции, он становится обозримым образом соответствующего процесса, демонстрируя интервалы возрастания и убывания, а также точки, в которых достигаются экстремальные значения.

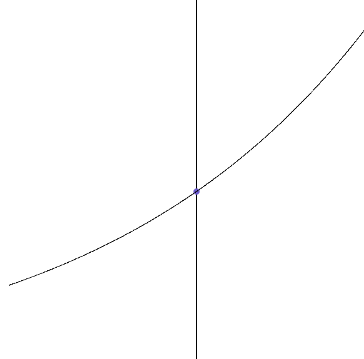
Напомним также, что с представлением о пластичном стержне связан такой важный и полезный объект прикладной математики как сплайн. Кроме того, используя соответствующий образ, можно с высокой степенью ясности объяснить, как графики функций от одной (рисунок 1) и двух (рисунок 2) переменных строятся компьютерными программами.

Рисунок 1

Рисунок 2

Пластичный стержень, превращаясь в график функции, изгибается в соответствии с формулой, которая задаёт эту функцию аналитически. Однако итоговая форма графика обычно предъявляется студенту как само собой разумеющаяся. Для некоторых элементарных функций полезно более подробно пояснить, почему данная функция имеет график именно такой формы. И здесь важную роль играют числовые последовательности.

Числовые последовательности в некотором смысле обозримы не хуже, чем графики функций. Пусть рассматривается последовательность {

a_{i}

}. Размещение на декартовой плоскости точек с координатами (

i; a_{i}

) часто позволяет увидеть связь данной последовательности с некоторой элементарной функцией. Так арифметическая прогрессия, очевидно, связана с линейной функцией (рисунок 3), а геометрическая – с показательной (рисунок 4).

Рисунок 3

Рисунок 4

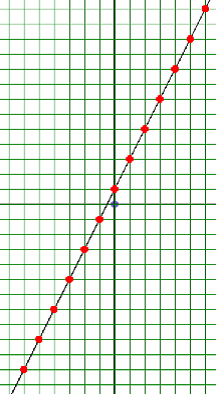
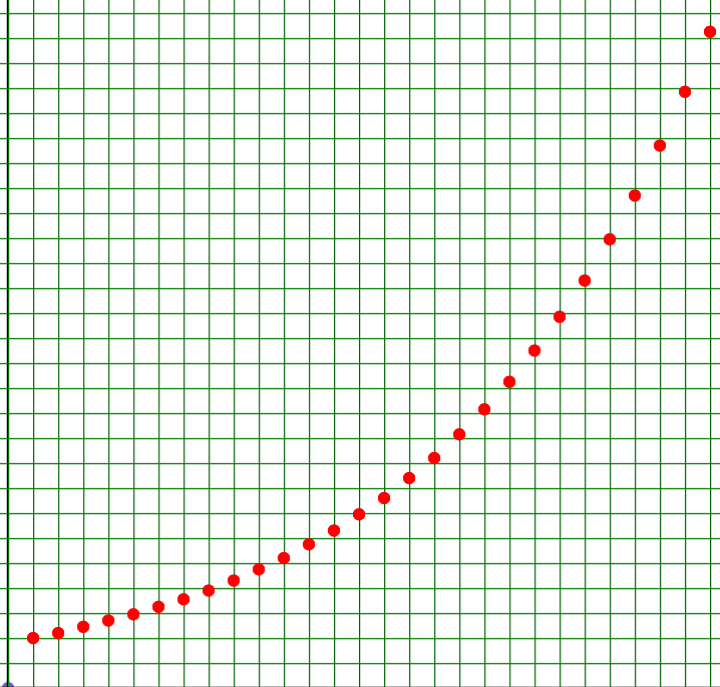
Более того, арифметическую прогрессию можно уплотнить до непрерывной линии (прямой), последовательно вставляя между её членами новые, которые являются средними арифметическими соседних членов. Геометрическая прогрессия до графика показательной функции уплотняется с помощью вычисления среднего геометрического соседних членов [23].

Рассмотрим операцию уплотнения более подробно.

Задание 1. Пусть на концах отрезка

[0; 1]

заданы значения функции

1

и

a

. Проведём уплотнение функции следующим образом. Сначала в аргументу

\frac{1}{2}

поставим в соответствие значение функции, равное среднему геометрическому концевых значений. Далее аналогичные уплотнения проведём для отрезков

[0; \frac{1}{2}]

и

[\frac{1}{2}; 1]

. Продолжим уплотнение для системы всё новых отрезков, убывающих по длине. Написать компьютерную программу уплотнения функции по этому алгоритму и построения соответствующего графика.

Решение. Программа, используя описанный алгоритм, заполняет два массива – массив абсцисс и массив ординат. Каждый из массивов содержит

2^{m}

элементов. Первоначально задаются только значения первого и последнего элементов каждого массива. Затем происходит постепенное заполнение массивов, сопровождающее деление очередных отрезков пополам. Для большей узнаваемости показательной функции

y = 2^{x}

уплотнение проводится на отрезке

[- 1; 1]

.

GraphicsWindow.Width = 620

GraphicsWindow.Height = 620

xb0 = 310

yb0 = 610

GraphicsWindow.DrawLine(xb0,0,xb0,620)

GraphicsWindow.DrawLine(0,yb0,620,yb0)

GraphicsWindow.FillEllipse(xb0-5, yb0-5,10,10)

ed = 300

GraphicsWindow.FillEllipse(xb0-5, yb0-ed-5,10,10)

m = 12

n = Math.Power(2,m)

x[0] = -1

x[n] = 1

y[0] = 1/2

y[n] = 2

For i = 0 To m-1

s = n / Math.Power(2,i)

For j = 0 To n - s Step s

x[j + s/2] = (x[j] + x[j+s])/2

y[j + s/2] = Math.SquareRoot(y[j]*y[j+s])

EndFor

For k = 0 To n

xe = xb0 + x[k]*ed

ye = yb0 - y[k]*ed

GraphicsWindow.SetPixel(xe,ye,"")

EndFor

Результат работы программы показан на рисунке 5.

Рисунок 5

Задание 2. Рассмотрим показательную функцию

y = a^{x}

и выберем на оси абсцисс произвольный отрезок

[x_{1}; x_{2}]

. Доказать, что построенные по предыдущему алгоритму уплотнения точки образуют геометрическую прогрессию и лежат на графике показательной функции.

Решение. Значение функции на концах отрезка равны

y_{1} = a^{x_{1}}

и

y_{2} = a^{x_{2}}

. Среднее геометрическое этих значений соответствует середине отрезка, то есть аргументу

\frac{x_{1} + x_{2}}{2}

. Кроме того, оно равно

y = \sqrt{y_{1} ∙ y_{2}}

=

\sqrt{a^{x_{1}} ∙ a^{x_{2}}} = a^{\frac{x_{1} + x_{2}}{2}}

. Таким образом, уплотняющая точка лежит на графике показательной функции

y = a^{x}

. Это рассуждение сохраняет свою силу при всех последующих уплотнениях. Поскольку уплотняющие аргументы отстоят друг от друга на равные расстояния, значения показательной функции, соответствующие им, образуют геометрическую прогрессию.

Задание 3. Пусть на концах отрезка

[x_{1}; x_{2}]

заданы значения функции

a

и

b

. Написать компьютерную программу уплотнения функции на отрезке с помощью среднего гармонического. Определить вид, возникающей функции.

Решение. Среднее гармоническое величин

a

и

b

является обратной величиной к среднему арифметическому обратных величин

\frac{1}{a}

и

\frac{1}{b}

. Вычисляется среднее гармоническое по формуле

s = \frac{2}{\frac{1}{a} + \frac{1}{b}} = \frac{2 ab}{a + b}

. Соответствующую программу можно получить из предыдущей заменой строки, в которой вычисляется среднее геометрическое, на строку, производящую вычисление среднего гармонического.

Чтобы установить вид функции, получаемой после уплотнения, отметим тот факт, что при уплотнении аргументы функции не используются. Таким образом, отрезок

[x_{1}; x_{2}]

можно задавать произвольно. Это означает, что при уплотнении строится класс функций, получаемых сдвигами и растяжениями оси абсцисс.

Что касается вида функции, возникающей при уплотнении, догадаться о нём можно, исходя из того, что среднее гармоническое является обратной величиной к среднему арифметическому обратных величин. Можно предположить, что

y = \frac{1}{x}

. Тогда при заданных значениях функции

a

и

b

аргументы принимают значения

x_{1} = \frac{1}{a}

и

x_{2} = \frac{1}{b}

. При уплотнении будет получено значение функции, равное

\frac{2}{\frac{1}{a} + \frac{1}{b}} = \frac{2}{x_{1} + x_{2}}

=

\frac{1}{\frac{x_{1} + x_{2}}{2}}

, то есть предположение является верным.

Задание 4. Придумать способ уплотнения последовательности для получения функции

y = x^{2}

с использованием стандартных средних величин – среднего арифметического и среднего геометрического.

Решение. Как уже было сказано, процедура уплотнения связана с вычислением значения функции в середине отрезка

[x_{1}; x_{2}]

. Рассмотрим, что получится в случае функции

y = x^{2}

. Отметим, что её значения на концах отрезка

[x_{1}; x_{2}]

равны

y_{1} = x_{1}^{2}

и

y_{2} = x_{2}^{2}

.

y (\frac{x_{1} + x_{2}}{2})

=

{(\frac{x_{1} + x_{2}}{2})}^{2} = \frac{x_{1}^{2} + x_{2}^{2}}{4} + \frac{x_{1} ∙ x_{2}}{2}

=

\frac{\frac{y_{1} + y_{2}}{2} + \sqrt{y_{1} ∙ y_{2}}}{2}

.

Таким образом, для получения функции

y = x^{2}

уплотнением следует использовать среднее арифметическое среднего арифметического и среднего геометрического концевых значений.

При изучении процедуры получения функций уплотнением последовательностей может возникнуть вопросы, которые можно сформулировать в виде заданий. Одна группа заданий аналогична заданию 4 и связана с поиском формулы уплотнения. Вторая группа заданий наоборот предполагает выяснение вида функций, получаемых при помощи заданной формулы уплотнения, например, следующее задание: «Можно ли выяснить, какая функция возникнет при уплотнении, основанном на вычислении среднего геометрического среднего арифметического и среднего геометрического концевых значений».

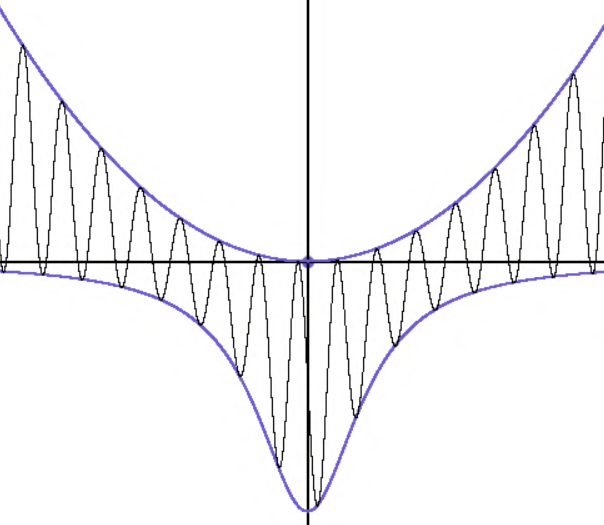
Что касается формы графиков синуса и косинуса, то в старых учебниках тригонометрии столь нелюбимых и осмеиваемых Дьедонне, давались наглядные изображения возникновения соответствующих волн при вращении радиуса-вектора. В наше время их можно получить на экране компьютера (рисунок 6).

Рисунок 6

Таким образом, существует несколько образных истолкований понятия функции, которые могут применяться при изучении математического анализа. Повторим, что обращение к этим представлениям возможно, но, конечно, необязательно. Преподаватель может обращаться к ним по мере надобности, особенно в индивидуальной работе, в частности, со студентами, имеющими проблемы со зрением.

Вопрос о форме графиков функций связан с исследованием возрастания и убывания функций, а также с поиском экстремумов функции, то есть изучается непосредственно в стандартном курсе математического анализа. Но есть ещё целый ряд подходов к этому вопросу, в частности рассмотрение задач на создание функций, графики которых имеют заданную форму, а сами функции заданы аналитически. Соответствующую деятельность можно назвать конструированием функций. В принципе именно конструирование функций используется в рамках такого предмета как «Вычислительная математика» при решении задач об интерполяции и аппроксимации функций. В качестве примеров можно привести получение формул для интерполяционного многочлена Лагранжа и кубических сплайнов.

Однако ряд задач на конструирование функций можно предложить студентам первого курса. Такие задачи позволяют уловить связь между аналитическим заданием функций и их пластическими образами (графиками). Конечно основным видом функций, используемых при конструировании, являются многочлены и дробно-рациональные функции. Приведём несколько примеров. Некоторые задания в силу их простоты будут приведены без решения.

Задание 5. Придумать функцию с заданными корнями.

Задание 6. Придумать функцию с заданными корнями и заданными вертикальными асимптотами.

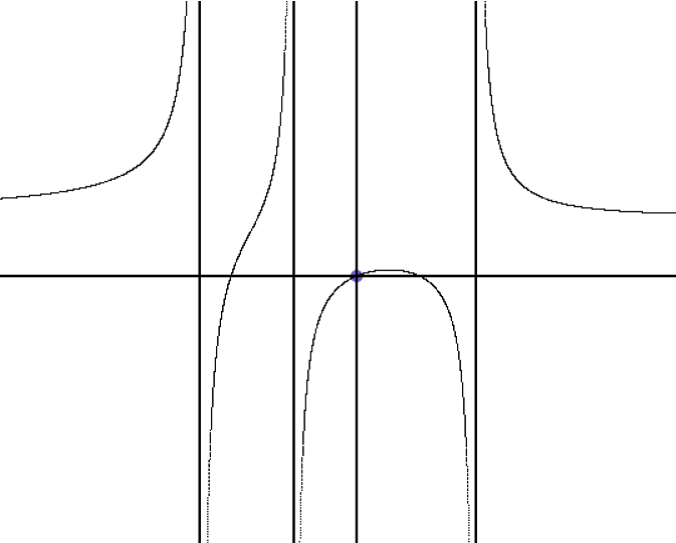
Решение. Искомая функция является отношением двух многочленов. Корни числителя одновременно являются корнями функции, а корни знаменателя определяют местоположение вертикальных асимптот. Приведём программу построения графика подобной функции с тремя корнями и тремя вертикальными асимптотами. Результат её работы показан на рисунке 7.

x0 = 320

y0 = 220

ed = 50

GraphicsWindow.FillEllipse(x0-5,y0-5,10,10)

GraphicsWindow.DrawLine(0,y0,640,y0)

GraphicsWindow.DrawLine(x0,0,x0,440)

'Корни функции

x1 = -2

x2 = 0

x3 = 1

'Асимптоты

a1 = -2.5

a2 = -1

a3 = 1.9

GraphicsWindow.DrawLine(x0+a1*ed,0,x0+a1*ed,440)

GraphicsWindow.DrawLine(x0+a2*ed,0,x0+a2*ed,440)

GraphicsWindow.DrawLine(x0+a3*ed,0,x0+a3*ed,440)

For x = -6 To 6 Step 0.001

p = (x - x1)*(x - x2)*(x - x3)

q = (x - a1)*(x - a2)*(x - a3)

If Math.Abs(q)>0.01 Then

y = p/q

xe = x0 + x*ed

ye = y0 - y*ed

GraphicsWindow.SetPixel(xe,ye,"")

EndIf

EndFor

Рисунок 7

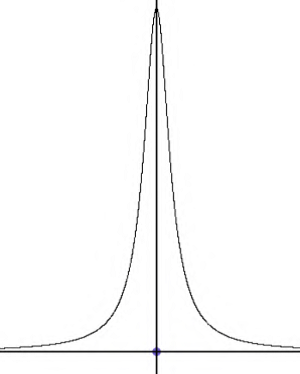
Задание 7. Придумать функцию, график которой похож на бугор на равнине.

Решение. Если бы конструировалась функция, которая могла уходить в бесконечность, то можно было бы использовать функции из предыдущего задания, например, функцию

\frac{1}{x^{2}}

. Однако функция должна быть ограничена, следовательно, знаменатель не может обращаться в ноль. Чтобы добиться этого, достаточно прибавить к знаменателю небольшое положительное число. Результат работы программы, строящей график такой функции, показан на рисунке 8.

x0 = 320

y0 = 410

ed = 50

GraphicsWindow.FillEllipse(x0-5,y0-5,10,10)

GraphicsWindow.DrawLine(0,y0,640,y0)

GraphicsWindow.DrawLine(x0,0,x0,440)

For x = -6 To 6 Step 0.001

p = 1

q = x*x + 1/8

y = p/q

xe = x0 + x*ed

ye = y0 - y*ed

GraphicsWindow.SetPixel(xe,ye,"")

EndFor

Рисунок 8

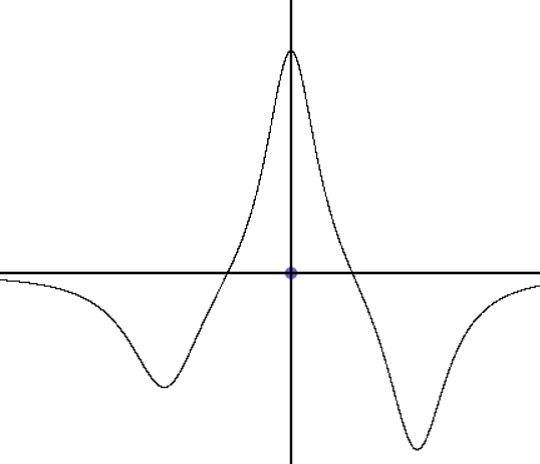
Задание 8. Придумать функцию, график которой даёт очертание вершин и впадин.

Решение. Впадина создаётся функцией, аналогичной бугру, но со знаком минус. Конструируемая функция является суммой бугров и впадин (рисунок 9).

x0 = 320

y0 = 220

ed = 50

GraphicsWindow.FillEllipse(x0-5,y0-5,10,10)

GraphicsWindow.DrawLine(0,y0,640,y0)

GraphicsWindow.DrawLine(x0,0,x0,440)

For x = -6 To 6 Step 0.001

p = 1

q1 = x*x + 1/4

q2 = -(x-2)*(x-2) - 1/3

q3 = -(x+2)*(x+2) - 1/2

y = p/q1 + p/q2 + p/q3

xe = x0 + x*ed

ye = y0 - y*ed

GraphicsWindow.SetPixel(xe,ye,"")

EndFor

Рисунок 9

В задании 8 был использован сдвиг функций вдоль оси абсцисс. Это обстоятельство показывает, что при конструировании функций могут использоваться различные преобразования. Изучение преобразований и само по себе является важной сферой, которая позволяет понять, взаимосвязь некоторых видов функций между собой. При этом естественным образом в рассмотрение вводятся различные семейства функций.

Уже в школьном курсе рассматриваются преобразования, задаваемые формулами вида

y = a ∙ f (ω ∙ (x - b)) + c

. Однако часто требуется более подробное знакомство с результатами их применения.

Задание 9. Построить гармонику высокой частоты, значения которой колеблются в пределах от нуля до единицы.

Задание 10. Построить семейство функций, графики которых деформируются, отправляясь от графика функции

y = f_{1} (x)

, в график функции

y = f_{2} (x)

.

Решение. Рассмотрим семейство вертикальных отрезков, соединяющих точки на соответствующих графиках. Множества точек, делящих каждый из таких отрезков в постоянном отношении. Как раз и образуют искомое семейство. Результат работы программы показан на рисунке 10.

x0 = 320

y0 = 220

ed = 50

GraphicsWindow.FillEllipse(x0-5,y0-5,10,10)

GraphicsWindow.DrawLine(0,y0,640,y0)

GraphicsWindow.DrawLine(x0,0,x0,440)

For x = -6 To 6 Step 0.001

y1 = - 4/(x*x +1)

xe = x0 + x*ed

ye1 = y0 - y1*ed

GraphicsWindow.FillEllipse(xe-1,ye1-1,2,2)

y2 = x*x/6

ye2 = y0 - y2*ed

GraphicsWindow.FillEllipse(xe-1,ye2-1,2,2)

EndFor

For t = 0 To 1 Step .1

For x = -6 To 6 Step 0.001

y1 = - 4/(x*x +1)

y2 = x*x/6

y = y1*t + y2*(1 - t)

xe = x0 + x*ed

ye = y0 - y*ed

GraphicsWindow.SetPixel(xe,ye"")

EndFor

Рисунок 10

Задание 11. Сконструировать функцию, график которой колеблется с определённой частотой между двумя функциями

y = f_{1} (x)

и

y = f_{2} (x)

.

Решение. Рассмотрим гармонику из задания 9 и будем использовать её значения для деления вертикальных отрезков, как это делается в задании 10 (рисунок 11).

x0 = 320

y0 = 220

ed = 50

GraphicsWindow.FillEllipse(x0-5,y0-5,10,10)

GraphicsWindow.DrawLine(0,y0,640,y0)

GraphicsWindow.DrawLine(x0,0,x0,440)

For x = -6 To 6 Step 0.001

y1 = - 4/(x*x +1)

xe = x0 + x*ed

ye1 = y0 - y1*ed

GraphicsWindow.FillEllipse(xe-1,ye1-1,2,2)

y2 = x*x/6

ye2 = y0 - y2*ed

GraphicsWindow.FillEllipse(xe-1,ye2-1,2,2)

EndFor

For x = -6 To 6 Step 0.0001

y1 = - 4/(x*x +1)

y2 = x*x/6

t = (Math.Sin(10*x) + 1)/2

y = y1*t + y2*(1 - t)

xe = x0 + x*ed

ye = y0 - y*ed

GraphicsWindow.SetPixel(xe,ye"")

EndFor

Рисунок 11

Ещё раз повторим, что соответствующие задания кому-то могут показаться неуместными, поскольку студент должен свободно владеть понятием функции и без них. Если это действительно так, то, конечно, подобные задачи не нужны. Однако опыт преподавания показывает, что иногда нужно углублять понимание студентами такого базового понятия математического анализа, как функция. Кроме того, задания, имеющие характер рассмотренных выше, помогают ощутить функции как осязаемые и доступные для манипулирования с ними объекты. Важность такого восприятия функций можно подчеркнуть, процитировав слова Шарля Эрмита: «Я убежден в том, что числа и функции анализа не являются произвольным продуктом нашего духа. Я верю, что они лежат вне нас с той же необходимостью, как предметы объективной реальности, а мы обнаруживаем или открываем и исследуем их так же, как это делают физики, химики и зоологи» [24].

РАСШИРЕНИЕ ПРЕДСТАВЛЕНИЙ О ФУНКЦИЯХ

Тот факт, что понятие функции является центральным в математике, указывает на его сложность. И по этой причине приходится касаться большого числа вопросов, развивающих это понятие. Прежде всего, образный подход к понятию функции ни в коей мере не отменяет необходимости знать теоретико-множественное определение отображения.

Пусть заданы множества

X

и

Y

. Бинарное отношение между ними называется отображением

f

с областью определения

X

и областью значений

Y

, если оно сопоставляет каждому элементу

x \in X

единственный элемент

f (x) \in Y

. Это весьма общее определение резко расширяет представления о функциях.

Желательно дать студентам примеры функций, выходящие за пределы математического анализа функций одного действительного переменного. Речь может идти, например, о функциях комплексного переменного. Кроме того, следует упомянуть логические функции. Желательно при этом продемонстрировать их связь с функциями математического анализа, в том числе и от нескольких переменных.

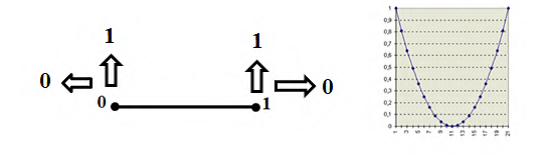
Скажем об этом несколько подробнее. Логическая функция от одного переменного связана с некоторыми функциями математического анализа, отображающими на отрезок [0; 1] в отрезок [0; 1]. Такие функции должны на концах отрезка [0; 1] принимать значения либо 0, либо 1 (рисунок 12).

Рисунок 12

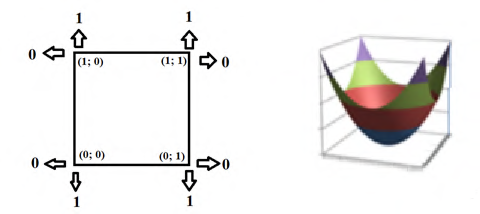
Аналогичное сопоставление можно продемонстрировать и для функций двух переменных (рисунок 13).

Рисунок 13

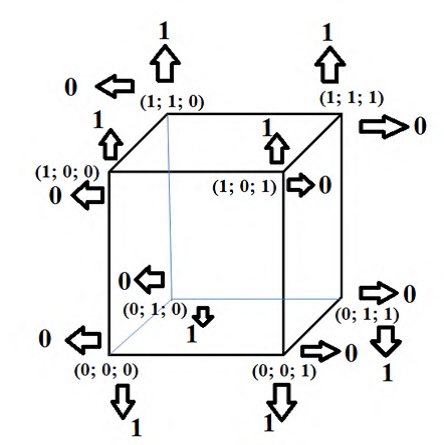
Наконец, можно продемонстрировать и схему построения логических функций трёх переменных, но уже без соответствующего аналога (рисунок 14).

Рисунок 14

Следующей темой может послужить вопрос о том, что описание кривых даже в рамках математического анализа выходит за пределы понятия функции. Это обстоятельство связано с единственностью элемента

f (x)

. Об этом будущие студенты узнают уже в школе при рассмотрении описания окружности с помощью неявного уравнения

x^{2} + y^{2} = r^{2}

. Чтобы в данном случае использовать понятие функции, окружность нужно разрезать на две ветви

y = \pm \sqrt{r^{2} - x^{2}}

. Однако в рамках школьной программы этот пример фактически является единственным.

В высшей школе количество таких примеров резко возрастает. Речь, в частности, идёт о кривых второго порядка и об описании различных кривых параметрическими уравнениями. Следует иметь в виду, что рассмотрение соответствующих вопросов приводит к освоению таких сложных понятий современной математики, как дифференцируемые многообразия.

Приведём пример задания на эту тему.

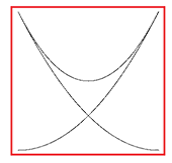
Задание 12. Дать параметрическое описание кривой, изображённой на рисунке 15.

Рисунок 15

Решение. Выясним, как меняются абсцисса и ордината точки, движущейся по данной кривой. Ордината убывает, пробегая значения из некоторого отрезка. Изменение абсциссы характерно для кубического многочлена с тремя корнями. Исходя из сказанного, опишем кривую уравнениями:

x = t ∙ (t^{2} - 4)

,

y = \frac{- t}{\sqrt{t^{2} + 1}}

.

Следующая программа подтверждает правильность проведённых рассуждений.

x0 = 320

y0 = 220

ed = 50

For t = -6 To 6 Step .001

x = t*(t-2)*(t+2)

y = -t/ Math.SquareRoot(t*t+1)

xe = x0 + x*ed

ye = y0 - y*ed

GraphicsWindow.SetPixel(xe,ye,"")

EndFor

Важным обстоятельством, связанным с изучением функций одного действительного переменного, является тот факт, что их описание в неявном виде требует использования функций двух переменных. Если задано неявное уравнение некоторой функциональной зависимости

F (x, y) = c

, то график соответствующей функции может быть построен как сечение поверхности

z = F (x, y)

горизонтальной плоскостью

z = c

. В рамках этой геометрической картины может быть проведено и рассмотрение неравенства вида

F (x, y) < c

.

Задание 13. Написать программу для построения сечения некоторой поверхности горизонтальной плоскостью. Изобразить область, координаты точек которой являются решением неравенства

F (x, y) < c

, а её граница является графиком функциональной зависимости

F (x, y) = c

.

Решение. В программе используется функция двух переменных

z = x^{4} + y^{4}

и функциональная зависимость

x^{4} + y^{4} = 1

. Результат работы программы показан на рисунке 16.

pi = Math.Pi

GraphicsWindow.Width = 600

GraphicsWindow.Height = 600

'Система аксонометрических координат

ed = 80

x0 = 300

y0 = 500

k = 1/3

ug = pi/5

x1 = x0 + ed* Math.Cos(ug)

y1 = y0 - ed* Math.Sin(ug)*k

x2 = x0 + ed* Math.Cos(ug+pi/2)

y2 = y0 - ed* Math.Sin(ug+pi/2)*k

x3 = x0

y3 = y0 - ed/2

'Декартова плоскость

For t1 = -1.5 To 1.5 Step .02

For t2 = -1.5 To 1.5 Step .2

t3 = 0

x = x0 + t1*(x1 - x0) + t2*(x2 - x0) + t3*(x3 -x0)

y = y0 + t1*(y1 - y0) + t2*(y2 - y0) + t3*(y3 -y0)

GraphicsWindow.SetPixel(x, y, "green")

EndFor

For t1 = -1.5 To 1.5 Step .2

For t2 = -1.5 To 1.5 Step .02

t3 = 0

x = x0 + t1*(x1 - x0) + t2*(x2 - x0) + t3*(x3 -x0)

y = y0 + t1*(y1 - y0) + t2*(y2 - y0) + t3*(y3 -y0)

GraphicsWindow.SetPixel(x, y, "green")

EndFor

'Область

For t1 = -1.5 To 1.5 Step .01

For t2 = -1.5 To 1.5 Step .01

t3 = t1*t1*t1*t1 + t2*t2*t2*t2

If t3 < 1 Then

x = x0 + t1*(x1 - x0) + t2*(x2 - x0)

y = y0 + t1*(y1 - y0) + t2*(y2 - y0)

GraphicsWindow.SetPixel(x, y, "red")

EndIf

EndFor

'Поверхность

For t1 = -1.5 To 1.5 Step .001

For t2 = -1.5 To 1.5 Step .3

t3 = t1*t1*t1*t1 + t2*t2*t2*t2

x = x0 + t1*(x1 - x0) + t2*(x2 - x0) + t3*(x3 -x0)

y = y0 + t1*(y1 - y0) + t2*(y2 - y0) + t3*(y3 -y0)

GraphicsWindow.SetPixel(x, y, "")

EndFor

For t1 = -1.5 To 1.5 Step .3

For t2 = -1.5 To 1.5 Step .001

t3 = t1*t1*t1*t1 + t2*t2*t2*t2

x = x0 + t1*(x1 - x0) + t2*(x2 - x0) + t3*(x3 -x0)

y = y0 + t1*(y1 - y0) + t2*(y2 - y0) + t3*(y3 -y0)

GraphicsWindow.SetPixel(x, y, "")

EndFor

Рисунок 16

Естественным продолжением заданий, связанных с конструированием функций, являются задачи, направленные на конструирование поверхностей.

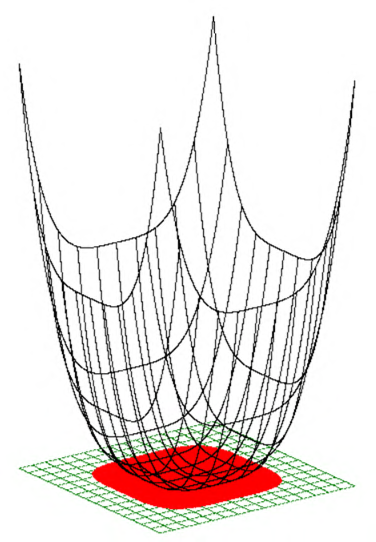
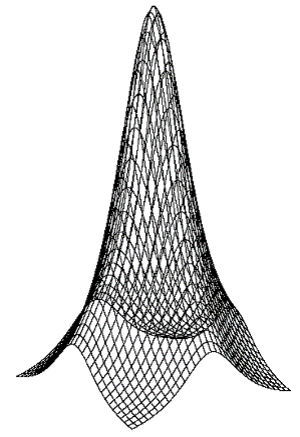
Задание 13. Сконструировать поверхность, моделирующую гору «Сахарная голова» в Рио-де-Жанейро (рисунок 17).

Рисунок 17

Рисунок 18

Решение. Используем в программе модифицированную функцию из задания 7. Результат работы программы показан на рисунке 18.

ВЫЧИСЛЕНИЯ И ОБРАЗЫ

До настоящего момента статья была посвящена развитию образа функции без рассмотрения более глубокой проблематики. Речь идёт об образном восприятии методов исследования функций. Общеизвестно насколько дифференцирование и интегрирования связаны с идеями геометрии и механики. Однако более или менее подробное рассмотрение этих вопросов в рамках данной статьи невозможно.

Ограничимся решением нескольких задач, чтобы показать сколь широким являются возможности образного подхода в рамках математического анализа. Начнём с двух простых задач, решения которых может быть получено без вычислений, но предполагают осмысления характера встречающихся в них функциональных зависимостей.

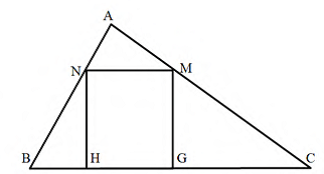
Задание 14. В треугольник вписать прямоугольник наибольшей площади (рисунок 19).

Рисунок 19

Решение. Поиск экстремума будет проведён без вычисления производной, а исходя из характера некоторых функции. Прямоугольник получается из треугольника

ABC

после отсечения от него треугольников

ANM

,

NBH

и

MGC

. При этом из двух последних треугольников можно сложить треугольник, подобный треугольнику

ANM

.

Площадь треугольника

ANM

пропорциональна квадрату длины отрезка

AN

, то есть её график можно рассматривать как параболу на отрезке АВ. Площадь подобного треугольника пропорциональна квадрату длины отрезка

BN

, то есть её график можно рассматривать как отражённую параболу на отрезке АВ. Сумма симметричных функций имеет минимум в середине отрезка (рисунок 20). Значения этой функции равны площади треугольника

ABC

минус площадь прямоугольника. Таким образом, прямоугольник имеет максимальное значение, когда отрезок

NM

является средней линией треугольника

ABC

.

Рисунок 20

Задание 15. Задана функция двух переменных z = x2 + y2. Найти её максимум и минимум в области (x – a)2 + (y – b)2

r2.

Решение. Рассмотрим точку

(x; y)

на декартовой плоскости. Тогда значение функции z = x2 + y2 в этой точке равно квадрату расстояния этой точки до начала координат. Из этого следует, что максимальное значение функции z в области, которая является кругом, достигается в самой далёкой от начала координат точке круга. Лежит эта точка на луче, проходящем через начало координат и центр круга

(a; b)

и находится соответствующей окружности. С минимумом дело обстоит аналогично, но только в том случае, когда начало координат не попадает в круг. Если же попадает, то минимум достигается как раз в начале координат.

Рассмотрим одно задание, при решении которого всё же придётся искать экстремум с помощью производной, однако, и здесь все рассуждения и вычисления можно провести устно.

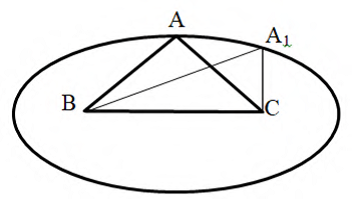
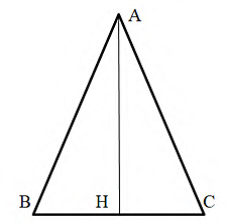
Задание 16. Среди треугольников с постоянным периметром найти тот, который обладает максимальной площадью.

Решение. Проведём решение в несколько этапов. Прежде всего, рассмотрим множество треугольников

ABC

с постоянным периметром и стороной

BC

фиксированной длины (рисунок 21). Найдём среди них треугольник наибольшей площади. Поскольку сумма сторон

AB

и

AC

постоянна, можно считать точки

B

и

C

фокусами эллипса, по которому перемещается точка

A

. Площадь треугольника

ABC

максимальна, когда максимальную длину имеет его высота. Из этого следует, что среди треугольников

ABC

с постоянным периметром и фиксированной стороной

BC

наибольшую площадь имеет равнобедренный треугольник.

Рисунок 21

На втором этапе вычислим квадрат площади равнобедренного треугольника с постоянным периметром (рисунок 22). Пусть полупериметр

AB + BH

такого треугольника равен

a

, а половина его основания

BH

равна

x

. Тогда по теореме Пифагора

{{AH}^{2} = AB}^{2} - {BH}^{2} = {(a - x)}^{2} - x^{2} = a^{2} - 2 ax

.

Рисунок 22

В итоге квадрат площади равнобедренного треугольника

ABC

равен

S

2

x^{2} ∙ (a^{2} - 2 ax)

=

x^{2} ∙ a^{2} - 2 a x^{3}

.

Наконец, находим производную данной функции, что без труда делается устно, приравниваем её к нулю и получаем, что максимум достигается при

x = \frac{a}{3}

. Таким образом, установлено, что среди треугольников с постоянным периметром максимальной площадью обладает правильный треугольник.

Задание 17. Провести исследование функции вида у = ах2 геометрическими методами.

Решение. Начнём с того, что отметим следующий простой факт. Если два прямоугольных треугольника АСВ и А1С1В1 подобны и, кроме того, АС =

\frac{1}{4 а}

, а ВС = А1С1 =

\frac{х}{2}

, то В1С1 = ах2 (рисунок 23).

Рисунок 23

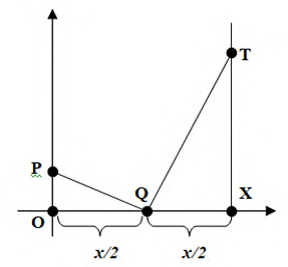
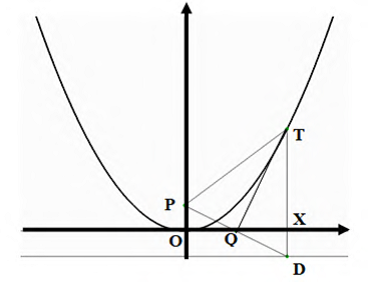
Далее рассмотрим геометрическую конструкцию, изображённую на рисунке 24, позволяющую строить любую точку параболы без вычислений

Рисунок 24

Поясним, как это осуществляется. Зафиксируем на координатной плоскости точку Р (0;

\frac{1}{4 а}

). Затем, выбрав произвольное значение х, зададим точки Q (

\frac{х}{2}

; 0) и X (х; 0) и построим треугольник РОQ. Далее через точку Х проведем вертикальную прямую, а через точку Q до пересечения с этой вертикалью в точке Т прямую QТ, перпендикулярную к прямой РQ. Прямоугольные треугольники РОQ и QХТ подобны, поскольку РQО = QТХ.

Теперь можно использовать отмеченный выше факт, согласно которому длина отрезка ХТ равна ах2, и, следовательно, точка Т лежит на параболе у = ах2.

Теперь можно доказать, что любая точка, лежащая на параболе у = ах2, равноудалена от точки Р (0;

\frac{1}{4 а}

), называемой фокусом параболы, и прямой у = –

\frac{1}{4 а}

, называемой директрисой параболы.

Упростим построение точки Т на параболе. На координатной плoскости выделим фокус Р и проведем директрису (рисунок 25). Выберем на оси абсцисс произвольную точку Х и проведем через нее вертикальную прямую до пересечения с директрисой в точке D.

Рисунок 25

Соединим точки Р и D отрезком. Он пересечет ось абсцисс в точке Q, являющейся серединой отрезка OX. Действительно, прямоугольные треугольники РQO и DQX равны, поскольку РО = ХD. способу построения фокуса и директрисы) и РQO = DQX (как вертикальные углы). Очевидно, что ОQ = QX и РQ = QD. Далее через точку Q проведем перпендикуляр к отрезку РD до пересечения с вертикалью ХD в точке Т. Эта точка, как доказано выше, лежит на параболе. Треугольники РQТ и DQТ являются прямоугольными. Катет QТ у них общий и РQ = QD. Значит, трeугольники равны, и, кроме того равны их гипотенузы РТ и ТD. Но длина отрезка РТ равна расстоянию от точки Т, лежащей на параболе, до фокуса Р, а ТD – перпендикуляр, опущенный на директрису, и его длина равна расстоянию от Р до директрисы. Итак, доказано, что парабола является геометрическим местом точек, равноудаленных от точки и прямой.

Отметим, что в аналитической геометрии параболу определяют именно, как такое геометрическое место точек. На его основании выводят уравнение параболы. Но наше исследование было проведено в обратном порядке – от уравнения у = ах2 к геометрической характеристике параболы.

Задание 18. Доказать, что в предыдущем задании прямая QТ является касательной к параболе у = ах2.

Решение. Написать уравнение прямой QТ. Далее следует показать, что система из двух уравнений, описывающих параболу и прямую QТ имеет единственное решение.

Задание 19. Дать геометрическое истолкование предела

e = lim_{n \to \infty} (1 + \frac{1}{n})^{n}

.

Решение. В дальнейших рассуждениях используем статью [14]. С показательной функцией связано число е. Это число в учебниках математического анализа обычно определяется как предел последовательности:

e = lim_{n \to \infty} (1 + \frac{1}{n})^{n}

. При этом не ясно, откуда эта последовательность возникла, и какова связь между этим определением числа е и определением числа е как основания степенной функции, имеющей в нуле производную равную единице.

В курсах математического анализа доказывается, что последовательность

(1 + \frac{1}{n})^{n}

является монотонно возрастающей и ограниченной. Из этого следует, что указанный предел, названный в честь Эйлера числом е, действительно существует. Доказательство ведётся с использованием бинома Ньютона. При этом выкладки студенту могут показаться довольно сложными, как и вообще любые вычисления, основанные исключительно на загадочной для новичка технике преобразований. Ему неясно, почему делается именно так, и как можно было именно это преобразование придумать.

Далее в курсе анализа устанавливается, что показательная функция, с основанием равным е, обладает замечательным свойством. Её производная равна самой этой функции, т. е.

(e^{x})^{'} = e^{x}

. Однако не совсем понятна причина этого обстоятельства: сначала вводится какой-то замысловатый предел, а его введение почему-то даёт такой удачный результат.

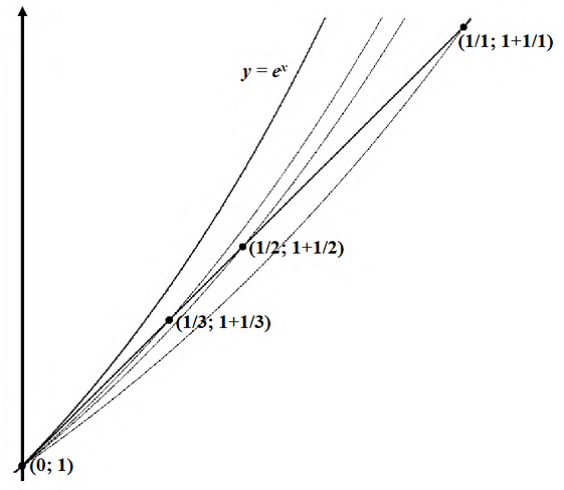
Дадим геометрическую интерпретацию соответствующего предела, позволяющую понять, откуда он появился. Начнём с перечисления очевидных фактов.

Графики всех показательных функций

y = a^{x}

(a > 1) проходят через точку (0; 1). Если a > b, то значения функции

y = a^{x}

при всех положительных значениях аргумента х больше значений функции

y = b^{x}

. Итак, показательная функция растёт тем быстрее, чем больше основание. Значит, при a > b функция

y = a^{x}

в точке х = 0 имеет производную большую, чем функция

y = b^{x}

в той же точке.

Если менять основание а показательной функции

y = a^{x}

в интервале от нуля до плюс бесконечности, то тангенс угла наклона касательных в точке х = 0 будет изменяться также в интервале от нуля до бесконечности. Это даёт нам основание назвать числом е такое основание показательной функции, для которого тангенс угла наклона касательной при х = 0 равен 1. Это второе определение числа е. Из всего сказанного следует, что такое число существует, поскольку, непрерывно меняясь в интервале от нуля до бесконечности, тангенс обязательно примет значение 1.

По известному определению касательная является предельным положением секущих в момент слияния двух точек пересечения в одну. Обычно это определение используется в отношении фиксированной функции.

Мы же поступим несколько иначе и будем искать одно за другим новые основания

a_{n}

показательных функций. При этом меняться будут функции, а секущая для всех графиков будет одна и та же: прямая с уравнением

y = x + 1

. Последовательность точек с координатами

(\frac{1}{n}; 1 + \frac{1}{n})

при n, стремящемся к бесконечности (n = 1, 2, 3, …) сходится к точке (0; 1). Основания же показательных функций

a_{n}

найдём, исходя из того, что функция

y = a_{n^{x}}

должна проходить через точку

(\frac{1}{n}; 1 + \frac{1}{n})

.

Итак, совпадающие секущие наклонены под углом 45º. Их вторая точка пересечения соответствует

x = \frac{1}{n}

, а первой всегда является х = 0. Таким образом, при изменении функций фиксированная секущая превращается в касательную итоговой функции.

Покажем, что последовательность

a_{n}

является монотонно возрастающей. Все точки графика функции

y = a_{n^{x}}

на отрезке [0;

\frac{1}{n}

] лежат ниже секущей (рисунок 26). В том числе и в точке

x = \frac{1}{n + 1}

. Значит, чтобы функция

y = a_{{n + 1}^{x}}

проходила через эту точку необходимо, чтобы выполнялось неравенство

a_{n + 1} > a_{n}

.

Рисунок 26

Теперь выясним, каким должно быть значение числа

a_{n}

. Точка с координатами

(\frac{1}{n}; (a_{n})^{\frac{1}{n}})

должна лежать на графике функции

y = a_{n^{x}}

. Далее, она должна обеспечить нужный наклон секущей, то есть

(a_{n})^{\frac{1}{n}} = 1 + \frac{1}{n}

. Следовательно,

a_{n} = (1 + \frac{1}{n})^{n}

. Итак,

e = lim_{n \to \infty} (1 + \frac{1}{n})^{n}

как раз по второму определению числа е.

Теперь связь между двумя определениями числа е становится понятной.

В заключение статьи вспомним слова знаменитого английского физика Уильяма Томсона (лорда Кельвина): «Математик – это тот, для кого равенство

\int_{- \infty}^{\infty} e^{- x^{2}} dx = \sqrt{π}

очевидно, как «2 × 2 = 4».

Эта цитата не безобидна. Она как минимум приводит начинающего математика в состояние недоумения: «Разве такое глубокое понимание математики возможно? Я не смогу достичь такого уровня». Конечно, можно назвать слова Кельвина преувеличением, но всё же хочется понять, в какой степени они истинны. Попробуем это сделать.

Слово «очевидно» в математике считается опасным. Когда математик занимается определённым вопросом и свободно ориентируется во всех взаимосвязях проблемы, он может считать что-то очевидным и написать об этом в статье. Через несколько лет, читая свою же статью, он полностью теряет ощущение очевидности. Тем не менее, некоторые вопросы для преподавателя очевидны, а для студента непонятны. Нужно полагать, что у преподавателя сформировано определённое образное пространства, в котором он может видеть (очевидеть, так сказать) внутренние связи математических идей и понятий. Студенту соответствующие представления нужно формировать.

Рассмотрим вопрос о вычислении интеграла

\int_{- \infty}^{\infty} e^{- x^{2}} dx

, не вдаваясь в детали, а пытаясь создать общую картину. При этом будут использованы более сложные чем в предыдущей части статьи математические понятия, такие как двойные и повторные интегралы, замена переменных, якобиан и т. д. При проведении рассуждений мы будем ориентироваться на книгу [25].

Сделаем ещё одно предварительное замечание. Ниже будет перечислено несколько положений, которые в совокупности позволяют увидеть, причину, по которой

\int_{- \infty}^{\infty} e^{- x^{2}} dx = \sqrt{π}

. Следует, однако, иметь в виду, что порядок перечисления может быть изменён. Таким образом, мы не проводим последовательное логическое рассуждение, а рисуем общую картину смыслового пространства, в котором путь к результату становится обозримым.

Интеграл $\int e^{- x^{2}} dx$ не берётся.
Интеграл $\iint e^{- (x 2 + y^{2}) dxdy}$ можно взять после перехода к полярной системе координат: $x = ρ ∙ \cos θ$ и $y = ρ ∙ \sin θ$ .
Замена переменных в двойном интеграле кроме замены переменных сопровождается умножением на соответствующий якобиан, то есть определитель матрицы из частных производных $x$ и $y$ по $ρ и θ$ .
Якобиан, связанный с переходом от декартовой системы координат к полярной равен $ρ$ .
Таким образом, если задана область G на декартовой плоскости, то

\iint_{G}^{} e^{- (x 2 + y^{2}) dxdy = \iint_{G}^{} ρ e^{- ρ^{2}} dρdθ}

6.Рассмотрим круговую область

B_{r} = {(x, y) : x^{2} + y^{2} \leq r^{2}}

. В ней выполняется равенство

\iint_{B_{r}}^{} e^{- (x 2 + y^{2}) dxdy = \int_{0}^{r} \int_{0}^{2 π} ρ e^{- ρ^{2}} dθdρ}

=

π ∙ (1 - e^{- r^{2}})

7.Рассмотрим квадратную область

C_{r} = [- r, r] \times [- r, r]

. В ней выполняется равенство

\iint_{C_{r}}^{} e^{- (x 2 + y^{2}) dxdy = {(\int_{- r}^{r} e^{- x^{2}} dx)}^{2}}

8.Если переходить от двойного интеграла по области к несобственному интегралу по всей декартовой плоскости, не имеет значения, как растёт область интегрирования – оставаясь квадратом или оставаясь кругом. Значит,

\lim_{r \to \infty} \iint_{C_{r}}^{} e^{- (x 2 + y^{2}) dxdy} = \lim_{r \to \infty} \iint_{B_{r}}^{} e^{- (x 2 + y^{2}) dxdy}

9.Рассмотрим эти пределы по отдельности. Первый равен по пункту 7

\lim_{r \to \infty} \iint_{C_{r}}^{} e^{- (x 2 + y^{2}) dxdy} = {(\int_{- \infty}^{\infty} e^{- x^{2}} dx)}^{2}

10.Второй равен по пункту 6

\lim_{r \to \infty} \iint_{B_{r}}^{} e^{- (x 2 + y^{2}) dxdy} = π

11.Получена формула

\int_{- \infty}^{\infty} e^{- x^{2}} dx = \sqrt{π}

.

Собрав всё изложенное в единый образ, можно почувствовать очевидность соответствующей формулы.

ЗАКЛЮЧЕНИЕ

Авторы статьи рассмотрели вопросы использования образов применительно к освоению понятия функции. При этом основное внимание было уделено развитию образа функции без рассмотрения более глубокой проблематики, связанной с дифференцированием, интегрированием, разложением функций в ряды и т. д. И это только те вопросы, которые связаны с математическим анализом. Естественно, что круг математической тематики за пределами анализа, требующей обращения к образам, значительно шире. Речь может идти о различных геометрических теориях – аналитической, проективной и неевклидовой геометрии, о линейной алгебре, теории дифференциальных уравнений, комплексном анализе и т. д. В дальнейшем авторы надеются рассмотреть соответствующий круг вопросов в новых статьях, сохранив главный принцип данной статьи: «Размышления и вычисления не должны противоборствовать. Они должны помогать друг другу».

Литература

Степанов М. Е. Образ силового поля как эвристическая модель в математике. Моделирование и анализ данных. Труды факультета информационных технологий МГППУ. – Вып. 3., 2007.
Степанов М. Е. Эрлангенская программа Клейна и геометрия треугольника. Моделирование и анализ данных. Труды факультета информационных технологий МГППУ. – 2015. №1. С.100-135.
Степанов М. Е. Эрлангенская программа Клейна и геометрия треугольника (часть вторая). Моделирование и анализ данных. Труды факультета информационных технологий МГППУ. – 2016. №1. С.60-115.
Степанов М. Е. Эрлангенская программа Клейна и геометрия треугольника Моделирование и анализ данных. Математическое образование. 2017. №3(83). С.28-42.
Степанов М. Е. Компьютерные технологии как средство приобщения учащегося к математической реальности. Моделирование и анализ данных. Научный журнал. – Вып. 1, 2018.
Куланин Е.Д., Нуркаева И.М.О двух геометрических задачах на экстремум. Математика в школе. 2019. № 4. С. 35-40.
Куланин Е.Д., Нуркаева И.М. Еще раз о задаче Мавло. Математика в школе. 2020. № 2. С. 76-79.
Куланин Е. Д., Степанов М. Е., Нуркаева И. М. Пропедевтика решения экстремальных задач в школьном курсе математики. Моделирование и анализ данных. 2019. № 4. С.127-144.
Куланин Е. Д., Нгуен Ву Куанг, Степанов М. Е. Осязаемая предметность с компьютерной поддержкой. Моделирование и анализ данных. Научный журнал. 2019. № 4. С.145-156.
Куланин Е. Д., Степанов М. Е., Нуркаева И. М. Роль образного мышления в научном мышлении. Моделирование и анализ данных. 2020. Т.10. №2 С.110 - 128.
Куланин Е.Д., Степанов М. Е., Нуркаева И.М. О различных подходах к решению экстремальных задач. Моделирование и анализ данных. 2020. Т.11. №1. С.40 - 60.
Лунгу К.Н., Норин В.П., Письменный Д.Т., Шевченко Ю.А., Куланин Е.Д. Сборник задач по высшей математике с контрольными работами. Москва, 2013. Том 2 (8-е издание).
Степанов М.Е. Из опыта работы в области тифлопедагогики. Моделирование и анализ данных. 2017. №1. С.42-53.
Степанов М.Е. Некоторые вопросы методики преподавания высшей математики. Моделирование и анализ данных. 2017. №1. С.54-94.
Куланин Е.Д., Степанов М. Е. Из опыта работы в режиме дистанционного обучения Моделирование и анализ данных. 2022. Т.12. №3. С.58 – 70.
Куланин Е.Д., Степанов М. Е. Всестороннее рассмотрение математических понятий как методический прием. Моделирование и анализ данных. 2022. Т.12. №4. С.67 – 84.
Куланин Е.Д., Степанов М. Е. О визуализации решений некоторых экстремальных задач. Моделирование и анализ данных. 2022. Т.12. №4. С.94 - 104.
Дьедонне Ж. Линейная алгебра и элементарная геометрия. М., Наука, 1972.
Гегель Г. В. Ф. Наука логики. Том 1. М., Мысль, 1970.
Лосев А. Ф. Диалектика мифа. М., Аст, 2021.
Арнольд В. И. О преподавании математики. Успехи математических наук. т. 53, вып.1 (319), 1998.
Витушкин А. Г. Оценка сложности задачи табулирования. М., Гос. изд. физ.-мат. лит., 1959.
Степанов М. Е. Об одном классе непрерывных функций. Моделирование и анализ данных. Труды факультета информационных технологий МГППУ. – Вып. 4, 2009.
Клайн М. Математика. Утрата определённости. М., Мир, 1984, с.372.
Спивак М. Математический анализ на многообразиях. М., Мир, 1968.

Информация об авторах

Куланин Евгений Дмитриевич, кандидат физико-математических наук, профессор, Московский государственный психолого-педагогический университет (ФГБОУ ВО МГППУ), Москва, Россия, ORCID: https://orcid.org/0000-0001-6093-7012, e-mail: lucas03@mail.ru

Степанов Михаил Евграфович, кандидат педагогических наук, доцент, Московский государственный психолого-педагогический университет (ФГБОУ ВО МГППУ), Москва, Россия, ORCID: https://orcid.org/0000-0003-4803-8211, e-mail: mestepanov@yandex.ru

Метрики

Просмотров

Всего: 0
В прошлом месяце: 0
В текущем месяце: 0

Скачиваний

Всего: 0
В прошлом месяце: 0
В текущем месяце: 0

PlumX

Метрики публикации