Измерение образовательных достижений пятиклассников по математике: связь с самооценкой и интересом

Измерение образовательных достижений пятиклассников по математике: связь с самооценкой и интересом

Введение

Образование является неотъемлемой частью становления личности . Каждый человек проходит через определенные социальные институты, в рамках которых формируется личность: детский сад, школа, университет, работа . Поэтому важно выбирать область обучения и работы в соответствии со своими интересами и желаниями [Eccles; Nezhnov] .

Сегодня обучение на специальностях STEM (Science, Technology, Engineering, Math) — один из приоритетных трендов в мировом образовании . Исследователи отмечают, что его развитие и поддержка являются важными направлениями образовательной политики [Модельный тренинг ООН—2015] Особенностью областей STEM при выборе образовательной и карьерной траекторий является важность математических знаний [Gall, 1999; Trauth] . В связи с этим необходимо уже в школе уделять достаточное внимание их оценке

В процессе обучения успеваемость по определенным предметам является отражением образовательных достижений учеников [Болотов] . Это приводит к определенному уровню самооценки и интересу к дальнейшему обучению В свою очередь, исследования показывают, что образовательные результаты по математике связаны с самооценкой личности [Shavelson] и интересом к этому предмету [Wigfield] .

Академическая самооценка формируется в процессе учебной деятельности и выступает механизмом регуляции Она проявляется в критическом отношении к себе, своим качествам, способностям и возможностям [Marsh] . Так, математическая самооценка относится к тому, в какой степени человек полагает, что способен преуспеть именно в этой деятельности по сравнению с другими [Simpkins] . В то же время познавательный интерес определяет академическую самооценку [Schiefele; Skaalvik, а; Wigfield, а] . Интерес показывает то, что деятельность интересна сама по себе без стимулирующих внешних факторов [Desjardins] .

В процессе получения образования происходит формирование самооценки, а также выделяется познавательный интерес Исследования показывают, что высокая академическая самооценка и интерес связаны с высокими образовательными результатами студентов и старших школьников [Correll; Skaalvik, а; Tai] . Например, высокая академическая самооценка характерна для «отличников» [Зайцев] . Они лучше воспринимают себя и свои способности, становятся более открытыми [Аминов] . Между тем избирательное и осознанное отношение к своим способностям и школьным предметам формируется у учащихся в начале средней школы [Ильин, 2000; Skaalvik] Это приводит к дифференциации интересов — учебно-профессиональная деятельность становится ведущей в юношеском возрасте [Давыдов, 2004] Мы считаем, что это может быть связано с тем, что при переходе в пятый класс школьник становится участником образовательного процесса нового типа: если на протяжении предыдущих четырех лет все образовательные дисциплины преимущественно вел один учитель, то в пятом классе разные образовательные дисциплины ведут разные учителя . Учитывая возрастные особенности формирования познавательного интереса у учеников, мы видим необходимость оценить вклад этого конструкта в измерение связи между самооценкой и образовательными достижениями

В нашей работе мы отвечаем на следующий исследовательский вопрос: как образовательные достижения пятиклассников по математике связаны с математической самооценкой при контроле интереса? Для этого мы используем данные личностного опросника, а также результаты образовательного теста по математике На основе этих данных мы проверяем модель, в которой интерес к математике является модератором связи между самооценкой и образовательными достижениями

Исследования показывают, что академическая самооценка связана с образовательными достижениями [Эльконин; Denissen; Ma; Marsh, а] . Например, ученики с высоким уровнем математической самооценки, как правило, достигают более высоких результатов по математике [Marsh, а] При этом данная связь может изменяться в процессе получения образования [Helmke; Skaalvik] Так, с возрастом также происходит снижение математической самооценки [Fredricks; Frenzel] . Это может объясняться тем, что младшие школьники более оптимистичны в оценивании своих способностей и возможностей их развития [Nicholls] . В процессе взросления школьники лучше определяют свою компетентность в определенных областях, сравнивая себя с одноклассниками . При этом снижение самооценки зафиксировано именно в отношении математики и естественных наук, но не в отношении гуманитарных предметов [Skaalvik, а] .

Познавательный интерес проявляется в процессе обучения и расширяет сферу познания . Интерес определяет предпочтения различной учебной деятельности, в частности, определенных предметов, и характеризуется положительными эмоциями в процессе познания [Савина] .

Мета-аналитическое исследование показало, что между интересом и образовательными достижениями есть статистически значимая связь [Schiefele, а] При этом в отдельных исследованиях связи интереса и образовательных достижений были отмечены противоречивые результаты . Согласно работе Р. С . Гардне­ра, Р. Н . Лалонде, Р . Муркрофт и Ф.Т. Эверс (R . C . Gardner, R . N . Lalonde, R . Moorcroft, F . T . Evers), между интересом к гуманитарным предметам есть связь, но она слабая [Gardner] . В схожем исследовании был получен другой результат: интерес являлся предиктором образовательных результатов по естественнонаучным дисциплинам [Yu]

Стоит отметить, что в процессе взросления интерес к изучению математики снижается . Это можно объяснить общим трендом, который наблюдается у школьников: со временем они становятся менее включенными в академическую активность [Epstein], интерес к учебе вытесняется социальными интересами, направленными на общение со сверстниками [Berndt; Эльконин] .

При переходе из начальной школы в основную часто наблюдается резкое снижение успеваемости школьников под воздействием самых разных факторов На наш взгляд, именно поэтому важно исследовать специфику образовательных результатов школьников именно на данном этапе: чтобы не «упустить» ребенка с высокими образовательными результатами, важно понимать, как стимулировать его познавательную активность

Неотъемлемым является тот факт, что и самооценка, и интерес могут изменяться в течение жизни . Согласно Л . С . Выготскому, возрастные периоды характеризуются особым отношением к обучению, которое специфично именно для данного возраста и определяет его познавательный интерес [Выготский, 1956]

Основываясь на результатах описанных исследований, мы выдвигаем несколько предположений:

— Гипотеза 1: у учеников пятого класса наблюдается связь между уровнем самооценки и образовательными достижениями

— Гипотеза 2: у учеников пятого класса наблюдается связь между познавательным интересом и образовательными достижениями

—  Гипотеза 3: у учеников пятого класса связь между самооценкой и образовательными достижениями опосредуется познавательным интересом

Программа исследования

В качестве инструментов были использованы: (1) личностный опросник для измерения уровня математической самооценки и интереса, а также (2) результаты по математике по тесту SAM (Student Achievements Monitoring)1.

Личностный опросник состоит из двух частей: в первой части на основе 3 вопросов измерялась математическая самооценка, во второй части также на основе 3 вопросов оценивался интерес к математике Первая часть опросника основана на многофакторной модели измерения самооценки Г . В . Марша и Р . Шавелсона (H .W. Marsh, R . Shavelson) [Marsh, б]. Для второй части опросника за основу взяты утверждения для измерения интереса, которые используются в международном мониторинго­вом исследовании качества математического и естественнонаучного образования TIMSS (Trends in Mathematics and Science Study) 2 .Для выражения степени согласия с утверждениями по «математической самооценке» используется 5-балльная частотная шкала Ликерта, которая ранжируется от «нет, в большинстве случаев нет» (1) до «да, в большинстве случаев да» (5) Для выражения степени согласия с утверждениями по «интересу к математике» используется 4-балльная шкала Ликерта от «полностью не согласен» (1)    до «полностью согласен» (4) .

Психометрические характеристики опросника имеют приемлемые значения (табл ) Средние показатели трудности свидетельствуют о том, что в основном ученики не склонны выбирать крайние категории шкалы Средний показатель дискриминативности больше 0,4, следовательно, утверждения позволяют дифференцировать учеников в соответствии с выраженностью математической самооценки и интереса Утверждения также согласованы между собой, что подтверждается показателями надежности шкал

Тест SAM разработан российскими специалистами и основан на модели функционального развития Л С Выготского [Карданова, 2008] SAM состоит из 45 заданий, они оцениваются дихо­томически: за правильное решение начисляется 1 балл Для анализа результатов SAM первичные баллы переводятся в 1000-балльную шкалу Достижения учеников оцениваются по двум показателям: тестовому баллу и уровню, на котором находится ученик Согласно концепции SAM, выделяются четыре уровня освоения математики: нулевой уровень — до 430 баллов, первый уровень (формальный) — 431—500 баллов, второй уровень (рефлексивный) — 501—570 баллов, третий уровень (функциональный) — выше 571 балла [Nezhnov] . Было показано, что тест SAM — валидный и надежный инструмент для измерения достижений по математике у школьников [Карданова, 2008] . Ключевым преимуществом SAM, выделяющим данный инструмент среди других средств измерения школьных достижений учащихся, является опора на систему представлений о возможных качественных уровнях (ступенях) образовательных достижений Систематизи­ровав результаты учеников, можно составить структурную компетентностную модель усвоения участниками исследования школьной программы и сформулировать соответствующие рекомендации по дальнейшему обучению В выборку исследования вошли 316 пятиклассников из трех общеобразовательных школ Республики Татарстан . Средний возраст учащихся — 11 лет (SD=0 . 33), из них 56% — девочки .

Инструменты исследования предъявлялись ученикам в бумажном виде в форме рабочих тетрадей Общее время на проведение исследования составляло 120 минут . Участники были осведомлены о целях и задачах исследования, также заранее было получено информированное согласие родителей

Для того чтобы проверить, является ли интерес к математике модератором связи между математической самооценкой и образовательными результатами, мы применяли метод моделирования структурными уравнениями (англ . structural equation modeling, SEM) . Анализ проводился в программном обеспечен

Таблица 

Психометрические характеристики опросника

ии STATA 13 . 0 . В качестве метода оценки параметров модели был применен метод максимального правдоподобия (англ . maximum likelihood, ML) .

В рамках использования метода моделирования структурными уравнениями соответствие модели эмпирическим данным проверяется при помощи нескольких статистик . Согласно эмпирическим исследованиям [Schreiber], удовлетворительной считается модель, для которой (1) соотношение статистики %2 к количеству степеней свободы меньше или равно 2; (2) сравнительный индекс соответствия (англ . comparative fit index, CFI) и индекс соответствия Такера-Льюиса (англ . Tucker Lewis index, TLI) больше или равны 0,95; (3) корень среднеквадратичной ошибки аппроксимации (англ . root mean square error of approximation, RMSEA) меньше 0,06 .

Результаты исследования

Построенная модель соответствует эмпирическим данным, %2 (14)=25,30, p>0,01. Согласно значениям статистик, модель имеет удовлетворительное качество: x2/df=25,30 (14), CFI=0,98, TLI=0,96, RMSEA=0,05.

Стандартизированные коэффициенты связи между переменными в модели, т е пути, варьируются от 0,00 до 0,83 . Все коэффициенты значимы на уровне p<0,001, за исключением пути между переменными «математическая самооценка» и «интерес к математике» . Обобщенная информация о стандартизированных коэффициентах связи представлена на путевой диаграмме ниже (рис )

Между математической самооценкой и образовательными результатами по данной дисциплине определена статистически значимая связь, p<0,001. Следовательно, уровень математической самооценки определяет результаты по этому предмету в школе, гипотеза 1 подтверждается

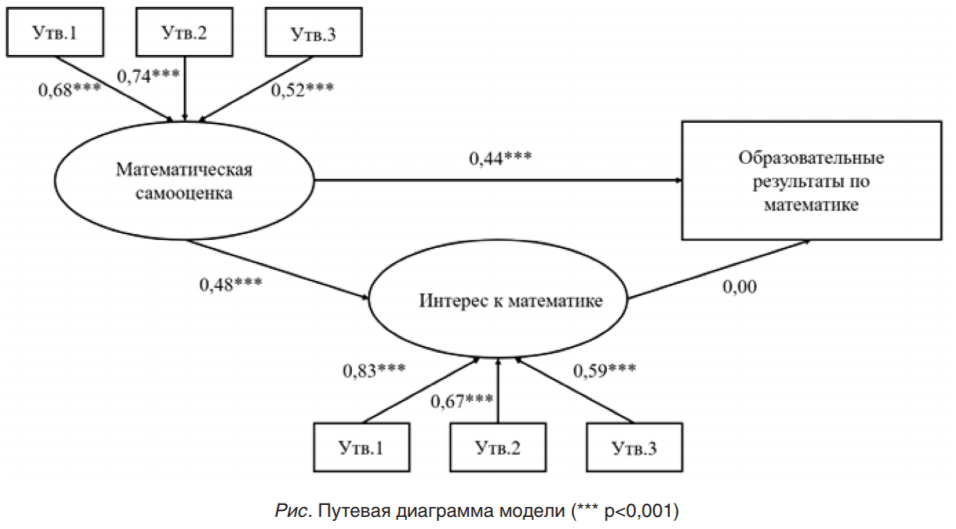
Аналогичный вывод получен и для связи двух других переменных — математической самооценки и интереса к данной дисциплине, p<0,001. То есть чем выше математическая самооценка, тем более выражен интерес к математике

Стоит отметить, что в построенной модели не была найдена статистически значимая связь между интересом к математике и образовательными достижениями по этому предмету, p>0,05 . Можно заключить, что для учащихся пятого класса как с наличием интереса к математике, так и с его отсутствием результаты по этому предмету будут одинаковыми, поэтому гипотеза 2 опровергается

В данной модели непрямой эффект связи между математической самооценкой и результатами по математике не модерируется интересом к этому предмету Стандартизированное значение непрямого эффекта невелико и статистически незначимо, p=0,74, гипотеза 3 не подтверждается