Проблема исследования.
В последнюю треть XX в. наблюдается значительный рост интереса к проблемам математического образования. Математические методы и математический стиль мышления наблюдаются в различных областях человеческой деятельности.
В развитии математических способностей большую роль играет формирование первых математических представлений. Многие авторы (П. Я. Гальперин, В. В. Давыдов, Н. И. Непомнящая и др.) отмечали, что успешный процесс овладения школьным курсом математики зависит от содержания и методов обучения детей старшего дошкольного и младшего школьного возраста. Ряд авторов (Р. Грин, В. Ларсон, М. Фидлер, Р. Хедрен и др.), создавая новые методики обучения начальной математике, опираются на работы Ж. Пиаже.
Однако, несмотря на существование разнообразных программ и методов обучения, несмотря на использование разнообразных технических средств, облегчающих выполнение математических операций, трудности в усвоении начальных математических понятий все же остаются у многих детей. Они возникают в младшей школе и часто сохраняются на протяжении всего школьного обучения, негативно влияя не только на развитие познавательных интересов и способностей ребенка, но и на становление его личностных качеств. В чем же причины данного явления?
Стремление приблизиться к пониманию этой проблемы побудило нас провести экспериментальное исследование, в котором приняли участие 46 детей.
Известно, что в последние годы увеличилось число детей с минимальными мозговыми дисфункциями, которые часто сопровождаются неврозами, повышением общей тревожности. У этих детей неизбежно страдают работоспособность, внимание, а нередко и высшие психические функции — память, восприятие, развитие речи, что не может не сказываться на усвоении математики. Цель данной работы — проанализировать трудности усвоения начального курса математики у таких детей.
Теоретические основы исследования
1. А. Р. Лурия о типах нарушения интеллектуальной деятельности в процессе решения арифметических задач.
Камень преткновения при усвоении школьной программы по математике — решение задач.
Процесс решения задач имеет сложное психологическое строение. Начинается он с анализа условий, в которых дана сформулированная в задаче цель, затем выделяются существенные связи, указанные в условиях, и создается схема решения.
После этого отыскиваются операции, необходимые для осуществления найденной схемы, а затем полученный результат сличается с исходными условиями задачи[9].
Достижение нужного эффекта возможно лишь при постоянном контроле за выполняемыми операциями. Течение этого сложного процесса может затрудняться в некоторых звеньях. Педагогам хорошо известно, что в большинстве случаев трудности при решении задач учащимися связаны с недостаточно тщательным анализом условий, с бесконтрольным построением неадекватных гипотез, с неоправданным применением стереотипных способов решения. Причиной ошибок нередко оказываются недостаточное внимание к сличению хода решения с исходными условиями задачи и лишь иногда — затруднения в вычислениях.
Подробное исследование анализа процесса решения задач описано А. Р. Лурией с соавторами[10] на примере взрослых пациентов с различной патологией мозга. Он ограничился изучением того, как страдает интеллектуальная деятельность при поражении задних (теменно-затылочных) и передних (лобных) отделов мозга. По его мнению, способность синтезировать отдельные элементы в сложные симультанные (пространственные) группы и возможность подчинить свое поведение исходному плану, обеспечив таким образом полноценную ориентировочную основу действия, составляют наиболее важные условия для решения задач.
Поражения задних (гностических) отделов мозговой коры, ответственных за блок приема, переработки и хранения информации, вызывают значительные нарушения таких операций, как: синтез последовательно поступающей информации в симультанные схемы, удержание поступающей информации в памяти, использование для переработки этой информации специальных речевых средств, успешное оперирование данными, хранящимися в памяти.
При всем этом сохраняется детальный анализ условий, интеллектуальная деятельность имеет направленный характер, результаты сличаются с исходными условиями, ошибки осознаются. Нарушенными оказываются, прежде всего, операции, с помощью которых решается задача.
Совсем другая картина нарушений интеллектуальной деятельности наблюдается при поражении лобных долей мозга — происходит изменение психической деятельности: задание не вызывает стойких намерений и не детерминирует протекание психических процессов; условия задачи не анализируются, не выделяются существенные элементы полученной информации, не сопоставляются входящие в условие компоненты задачи, нет общей схемы, программы решения задачи, исходящей из предварительного анализа ее условий.
Пациенты ограничиваются тем, что дают импульсивные ответы, с трудом переключаются с одной операции на другую, полученные результаты не сличают с исходными условиями задачи, ошибки не осознают и не исправляют, вся деятельность приобретает бесконтрольный характер.
Результаты, полученные при решении задач больными с локальными поражениями мозга, помогают вскрыть психологические механизмы звеньев интеллектуального акта, протекающего у детей при решении математических задач.
2. Анализ задач и алгоритмов их решения в теории А. Р. Лурии
Для получения информации о структуре интеллектуальной деятельности и ее изменениях при первичном нарушении различных входящих в ее состав факторов рассмотрим анализ относительно элементарных арифметических задач. Структуру решения задачи воспроизводит те черты, которые характеризуют любой интеллектуальный акт. Очевидно, что нарушение прочности удержания исходного условия, ослабление или нарушение ориентировочной основы действия, трудности в создании и удержании основного плана решения задачи, нарушение выполнения нужных операций, дефект в сличении полученных результатов с исходными условиями задачи — все это будет по-разному сказываться на процессе ее решения и может легко обнаружиться при внимательном анализе процесса решения. Однако успех исследования зависит также от подбора серии задач, алгоритмы решения которых отвечают известным требованиям и обеспечивают последовательное изучение интеллектуальной деятельности различной сложности.
В основу набора таких задач положен принцип последовательного усложнения алгоритма решения, влекущего за собой различные виды психологических затруднений[10].
- Простые задачи типа a+b=x или a—b=x. Например: «У Маши 5 яблок, у Пети 4 яблока. Сколько яблок у Маши и Пети вместе?» Подобные задачи могут быть решены одной арифметической операцией, и условие этих задач однозначно определяет алгоритм их решения.
- Простые, но инвертированные (косвенные) задачи типа a—x=b или x—a=b. Например: «У мальчика было 12 яблок, часть из них он отдал другу. У него осталось 8 яблок. Сколько яблок он отдал другу?» Необходимые в этих задачах операции не отличаются от тех, которые требовались в предыдущей группе задач. Однако психологическая структура существенно отличается. В инвертированных задачах порядок действий расходится с порядком, в котором предъявлялись данные условия. Решающий должен преодолеть тенденцию прямого решения задачи, и всякая повышенная инертность следов, возникающих от прочтения условия, может создать значительные затруднения.
- Составные задачи типа a+(a+b)=x или a+(a—b)=x. Например: «У Маши 5 яблок, а у Кати на 2 яблока больше. Сколько яблок у обеих девочек?» Существенная особенность этих задач в том, что решение одним непосредственно возникающим действием невозможно. Для правильного решения необходима определенная последовательность операций. Условие задачи непосредственно не определяет возможный ход ее решения. Нарушение предварительной ориентировки в условиях задачи легко приводит к упрощению ее структуры с заменой относительного значения второй величины на абсолютное.
- Сложные составные задачи типа a+(a+b)+((a+b)—c)=x. Например: «Сыну 15 лет. Отец на 25 лет старше сына. Мать на 5 лет моложе отца. Сколько лет им вместе?» Эти задачи содержат значительно большее число элементов, чем предыдущие. Существенно, что алгоритм их решения распадается на ряд последовательных операций, каждая из которых вытекает из предыдущей. Это приводит к необходимости производить весь цикл нужных операций, опираясь на запоминание результатов предшествующей операции и делая ее исходной для последующей. Усвоение отдельных данных, входящих в условие задачи, не определяет однозначно плана ее решения, нужная система действий должна быть выбрана из значительного числа возможных операций.
- Сложные задачи с инвертированным ходом действий типа: a+b=x, xm=y, y — b=z. Например: «Сыну 5 лет, через 15 лет отец будет в три раза старше сына. Сколько лет отцу сейчас?» Характерной особенностью задач этой группы является то, что все промежуточные операции не сформулированы в условиях задачи и ответ на конечный вопрос — это результат целой цепи проделанных вспомогательных операций. Торможение попыток непосредственного решения задачи, перенос основного внимания на нахождение серии вспомогательных операций, не сформулированных в условии задачи, осложнение последней инвертированной операцией — все это делает решение подобной задачи особенно сложным.
- Задачи типа x+y=a, nx+y=b. Например: «Одна ручка и один букварь стоят 37 копеек. Две ручки и один букварь стоят 49 копеек. Сколько стоят отдельно одна ручка и один букварь?» Эти задачи не могут быть решены прямой операцией деления суммы пополам и требуют вспомогательного приема. Решающий должен понять предъявляемые требования и затормозить попытки решить эти задачи с помощью непосредственных, ранее упроченных способов.
Сюда же относятся задачи, решение которых требует продуманной последовательности операций.
К перечисленным типам задач А. Р. Лурия[10] добавляет еще один вариант.
- «Конфликтные» задачи, формулировка которых наталкивает на неверное решение. К ним относятся все задачи, при решении которых необходимо выполнить операцию, не соответствующую стереотипу, в частности операцию, противоположную той, которая определяется семантикой входящих в условие слов. Например: «В кувшине было 7 литров молока, а после того как долили, стало 10. Сколько долили литров молока?», «На дереве сидели птицы. Сначала улетели 2 птички, затем еще 3. Сколько всего птиц улетело?» Глагол «долили» провоцирует ребенка произвести операцию сложения, а необходимо совершить противоположное действие. Аналогично глагол «улетели» провоцирует вычитание. Решение этих задач вызывает трудности у больных с «лобным синдромом».
Можно предположить, что эти задачи будут трудны и для детей с недостаточной сформированностью функций программирования и контроля произвольных действий.
Кроме того, А. Р. Лурия выделяет трудности решения задач у больных с поражением теменно-височно-затылочных отделов левого полушария. Обычно это задачи, в тексте которых используются грамматические структуры «столько..., сколько..,», «каждый из которых...», «на сколько больше(меньше)...», «во сколько раз больше(меньше)...». К этому же типу задач можно отнести следующие: «какое число следует за...», «какое число предшествует...», «найди число, которое на 7 меньше 9» и т. д. Сложными для понимания являются грамматические конструкции со словами «ниже», «тоньше», «мельче», «младше», «легче», «дешевле». Можно предположить, что эти задачи будут плохо решаться детьми с трудностями пространственной ориентировки и, следовательно, с нарушением восприятия логико-грамматических конструкций.
Описанные блоки задач наиболее типичны для различных учебников I класса школы.
3. А. Р. Лурия о системной локализации психических функций
А. Р. Лурия выделил в работе мозга три функциональных блока: I. Энергетический, регулирующий тонус мозга (состояние «сон — бодрствование»). II. Связанный с приемом, переработкой и хранением информации. III. Процессы программирования и контроля произвольных действий.
При развитии зон мозга существует определенная последовательность их формирования. Позже всего формируется третий блок. Поэтому чаще всего трудности встречаются при его формировании и связаны с программированием и контролем интеллектуальных действий. Это не позволяет школьникам решать задачи сложного типа, где необходима первичная ориентировка в условиях задачи, выполнение цепи последовательных операций, непосредственно не заданных в ее условии. Для этих детей основная сложность состоит в том, чтобы выстроить необходимую последовательность действий и затормозить выполнение действий, навязанных определенным стереотипом.
Достаточно часто нейропсихологическая диагностика позволяет обнаружить детей с незрелостью второго функционального блока, т. е. с различными пространственными нарушениями, зеркальностью, плохим пониманием логико-грамматических конструкций. Для них характерны ошибки по заднему (теменно-затылочному) типу. Они не всегда понимают формулировку условия задачи, им трудно понять такие логико-грамматические конструкции, как «во сколько раз...», «на сколько больше, чем...», «столько, сколько...» и т. д. Кроме того, нарушения пространственных представлений вызывают сложности в усвоении понятий «состав числа», «разряд», «переход через десяток при сложении и вычитании»[10].
Опираясь на теоретические положения А. Р. Лурии, мы поставили следующие задачи исследования:
- Выявить взаимосвязь трудностей усвоения начального курса математики (на примере решения арифметических задач) и нейропсихологического статуса ребенка.
- Выделить и проанализировать словесно-логическое содержание арифметических задач, которые вызывают трудности у детей младшего школьного возраста, испытывающих различные нейропсихологические трудности.
- Проверить понимание детьми логической обратимости на примере задач Ж. Пиаже.
- Проверить способность к сокращению действия у ребенка, хронически не успевающего по математике.
Общая гипотеза исследования Базисной причиной трудностей освоения математики может быть недоразвитие высших психических функций (ВПФ), в частности связанных со зрительно-пространственными представлениями, пониманием логико-грамматических конструкций (II блок, по А. Р. Лурии); развитием произвольности (III блок). Эти типы нарушений детально изучены в работах А. Р. Лурии и его учеников[9, 10, 2].
Частные гипотезы исследования.
Первая гипотеза. Трудности усвоения начального курса математики, в частности решение простых задач, связаны с вербальной формой предъявления задач. Можно предположить, что наибольшие трудности вызывают два типа задач: А. Задачи, содержащие несколько этапов решения. Для решения этих задач необходимо построить определенную программу действий. Б. Задачи, в формулировках которых обязательно содержатся сложные логико-грамматические конструкции.
Вторая гипотеза. Задачи типа А будут вызывать трудности у детей с нарушением функций планирования и контроля, типа Б — у детей с нарушением функций пространственного анализа и синтеза.
Третья гипотеза. Трудности в решении простых арифметических задач могут быть связаны у той и другой группы детей с отсутствием у ребенка конкретных логических операций, что можно обнаружить с помощью тестов Ж. Пиаже.
Четвертая гипотеза. Трудности в усвоении математики у детей, уже достигших стадии конкретных операций и не имеющих нейропсихологических нарушений, могут быть связаны с несформированностью в процессе обучения операций сокращения действия, что выявляется при исследовании способности ребенка к составлению разнообразных схем математического содержания задачи.
Проверка первой гипотезы
Согласно исходной гипотезе, наибольшие трудности вызывают два вида задач: А — задачи, для решения которых необходимо построить определенную программу действий, состоящую из нескольких шагов. Б — задачи, в формулировке которых содержатся сложные логико-грамматические конструкции.
Для проверки этой гипотезы были подобраны задачи из учебников для I класса, которые предъявлялись ученикам экспериментальной и контрольной групп.
В экспериментальную группу вошли 9 учеников I класса, обучавшихся в Комплексе педагогической реабилитации (дети с отставанием в развитии, диспропорциональным развитием ВПФ, соматически ослабленные). Все дети были обследованы психологом и нейропсихологом.
В контрольную группу вошли дети двух первых классов типичной московской школы (35 человек).
Каждому ребенку экспериментальной группы в ситуации обследования предлагалось решить 7 задач типа А и 10 задач типа Б, фиксировались время решения задачи, ход решения, ошибки, оказываемая помощь.
Общие результаты решения задач каждым ребенком экспериментальной группы отражены в таблице и на графиках.
В табл. 1 представлены результаты решения задач типа А и типа Б детьми экспериментальной группы. Отмечены задачи, решенные с помощью экспериментатора и самостоятельно.
Таблица 1 Ошибки в решении задач детьми экспериментальной группы (%)
|
Ученики
|
Задачи типа А (Решение без помощи)
|
Задачи типа А (Решение с помощью)
|
Задачи типа Б (Решение без помощи)
|
Задачи типа Б (Решение с помощью)
|
|---|---|---|---|---|
|
Камиль М.
|
86
|
14
|
60
|
20
|
|
Саша Ж.
|
43
|
0
|
60
|
30
|
|
Рауф А.
|
57
|
0
|
30
|
0
|
|
Денис Х.
|
29
|
14
|
20
|
0
|
|
Сережа Ф.
|
100
|
57
|
70
|
30
|
|
Дима П.
|
57
|
14
|
80
|
20
|
|
Саша Н.
|
43
|
0
|
50
|
10
|
|
Павел Г.
|
29
|
0
|
60
|
0
|
|
Артем П.
|
100
|
71
|
80
|
60
|
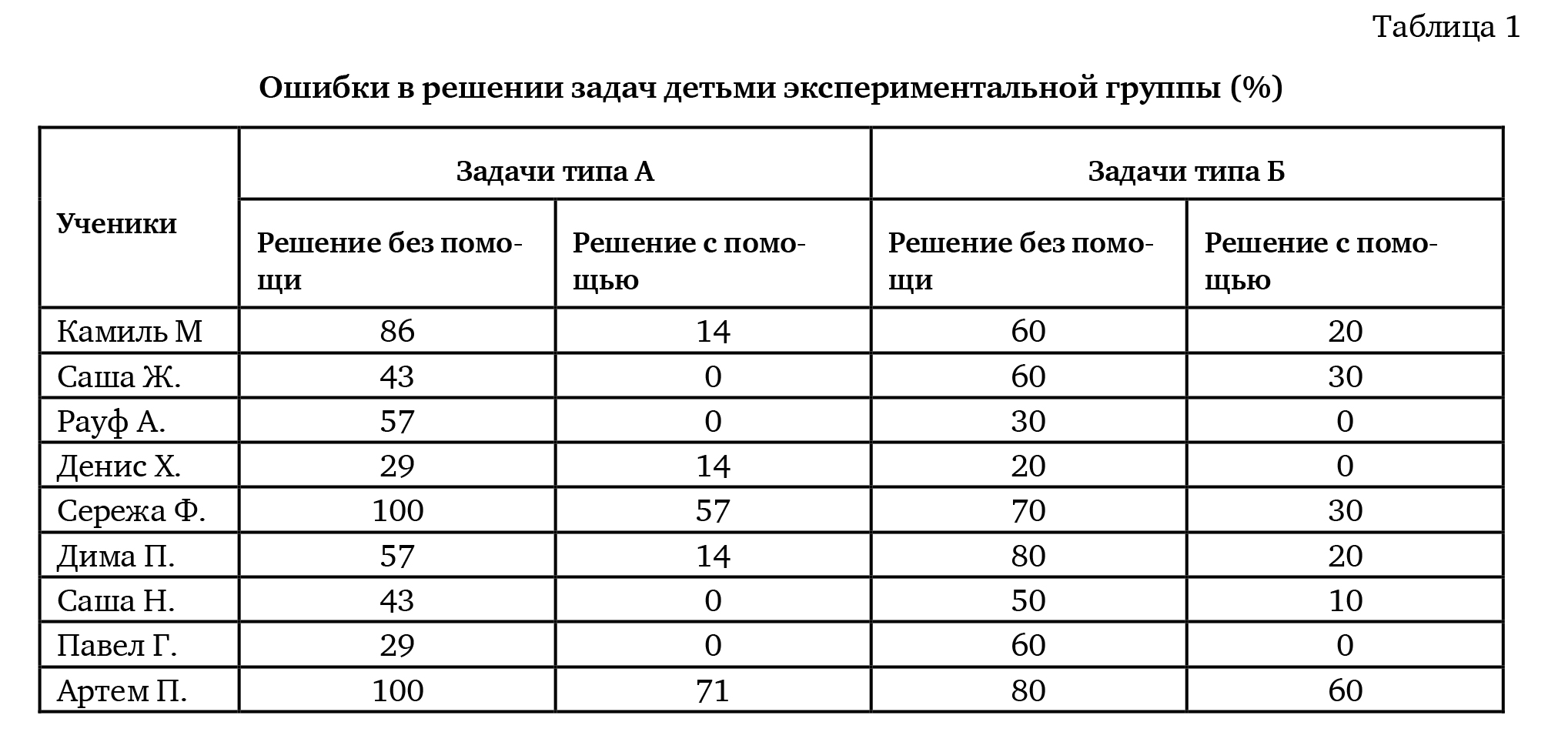
Из табл. 1 видно, что задачи типа А и типа Б вызывают большие трудности у всех детей экспериментальной группы.
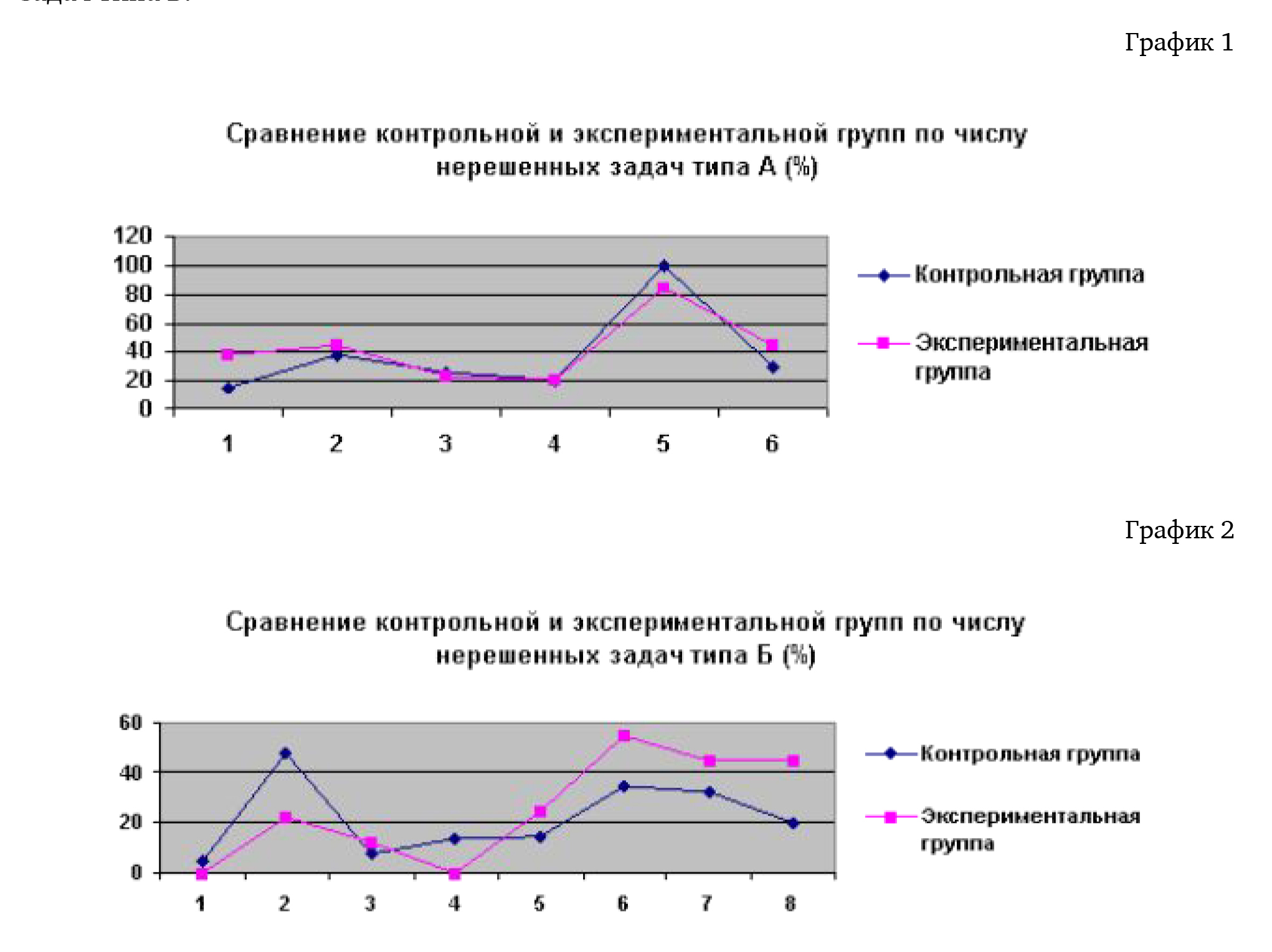
Сравнительные результаты решения задач детьми экспериментальной и контрольной групп представлены в графиках 1 и 2.
Из графика видно, что задачи типа А одинаково трудны для детей как контрольной группы (условная норма), так и экспериментальной (дети с нейропсихологическими нарушениями). Причем наибольшие трудности вызывают одни и те же задачи, в которых детям необходимо не только тщательно проанализировать условие, но и выстроить цепочку последовательных действий.
В то же время дети обеих групп хуже решают задачи с формулировками «перед», «легче», «ниже», чем с формулировками «за», «выше», «между».
На данном графике есть тенденция, отражающая большие трудности выполнения заданий типа Б именно учащимися общеобразовательной школы. Можно предположить, что это связано с тем, что учитель коррекционного класса (экспериментальная группа) специально тренировал понимание логико-грамматических конструкций.
Итак, анализ результатов показывает, что первая гипотеза получила подтверждение. Действительно, задачи типа А и типа Б трудны для учеников 1 класса. Но что лежит в основе эти трудностей?
Проверка второй гипотезы
В соответствии со второй гипотезой дети с нарушением функций планирования и контроля (по данным нейропсихологического обследования) будут испытывать трудности в решении задач типа А; дети с нарушением пространственного анализа и синтеза (по результатам нейропсихологического обследования) будут испытывать большие трудности в решении задач типа Б.
Дети с различными пространственными нарушениями, зеркальностью, плохим пониманием логико-грамматических конструкций не всегда ориентируются в формулировке условия задачи, для них трудны логико-грамматические конструкции со словами «во сколько раз...», «на сколько...», «больше, чем...», «столько, сколько...». Для них характерны сложности в усвоении таких понятий, как «состав числа», «разряд», «переход через десяток при сложении и вычитании».
Дети со сложностями программирования и контроля плохо решают задачи, где необходима первичная ориентировка в условии, выполнение цепи последовательных операций, непосредственно не вытекающей из данных условий. Для этих детей основная сложность состоит в том, чтобы выстроить необходимую последовательность действий и затормозить выполнение действий, навязанных определенным стереотипом.
У большинства детей наблюдаются оба вида трудностей, но в разных пропорциях. Это связано, в частности, с тем, что недоразвитие III блока ведет к вторичным изменениям в функционировании II блока, а отставание в развитии процессов переработки информации (II блок) — к вторичному запаздыванию в развитии функций программирования и контроля (III блок). Однако первичные дефекты у детей более стойки[1], и это отражается в решении задач.
Полученные данные по решению задач (в % ошибок) в ходе индивидуального обследования детьми экспериментальной группы соотнесены с результатами нейропсихологического обследования ребенка в табл. 2.
Таблица 2
|
Ученики
|
Задачи типа А (%)
|
Задачи типа Б (%)
|
Нейропсихологический диагноз
|
Типы задачи
|
|---|---|---|---|---|
|
Денис Х.
|
29
|
20
|
В основном трудности программирования и контроля
|
А
|
|
Артем П.
|
100
|
80
|
В основном трудности программирования и контроля
|
А
|
|
Саша Ж.
|
43
|
60
|
Трудности — пространственные представления, менее ярко — программирование и контроль
|
Б
|
|
Дима П.
|
57
|
80
|
В основном пространственные трудности
|
Б
|
|
Сережа Ф.
|
100
|
70
|
Трудности программирования и контроля, менее выраженные пространственные трудности
|
А, Б
|
|
Саша Н.
|
43
|
50
|
Трудности программирования и контроля, пространственные трудности
|
А, Б
|
|
Паша Г.
|
29
|
60
|
Трудности программирования и контроля, пространственные трудности
|
А, Б
|
|
Камиль М.
|
86
|
60
|
Трудности программирования и контроля, нарушены пространственные представления
|
А, Б
|
|
Рауф А.
|
57
|
30
|
Трудности программирования и контроля, нарушены пространственные представления
|
А, Б
|
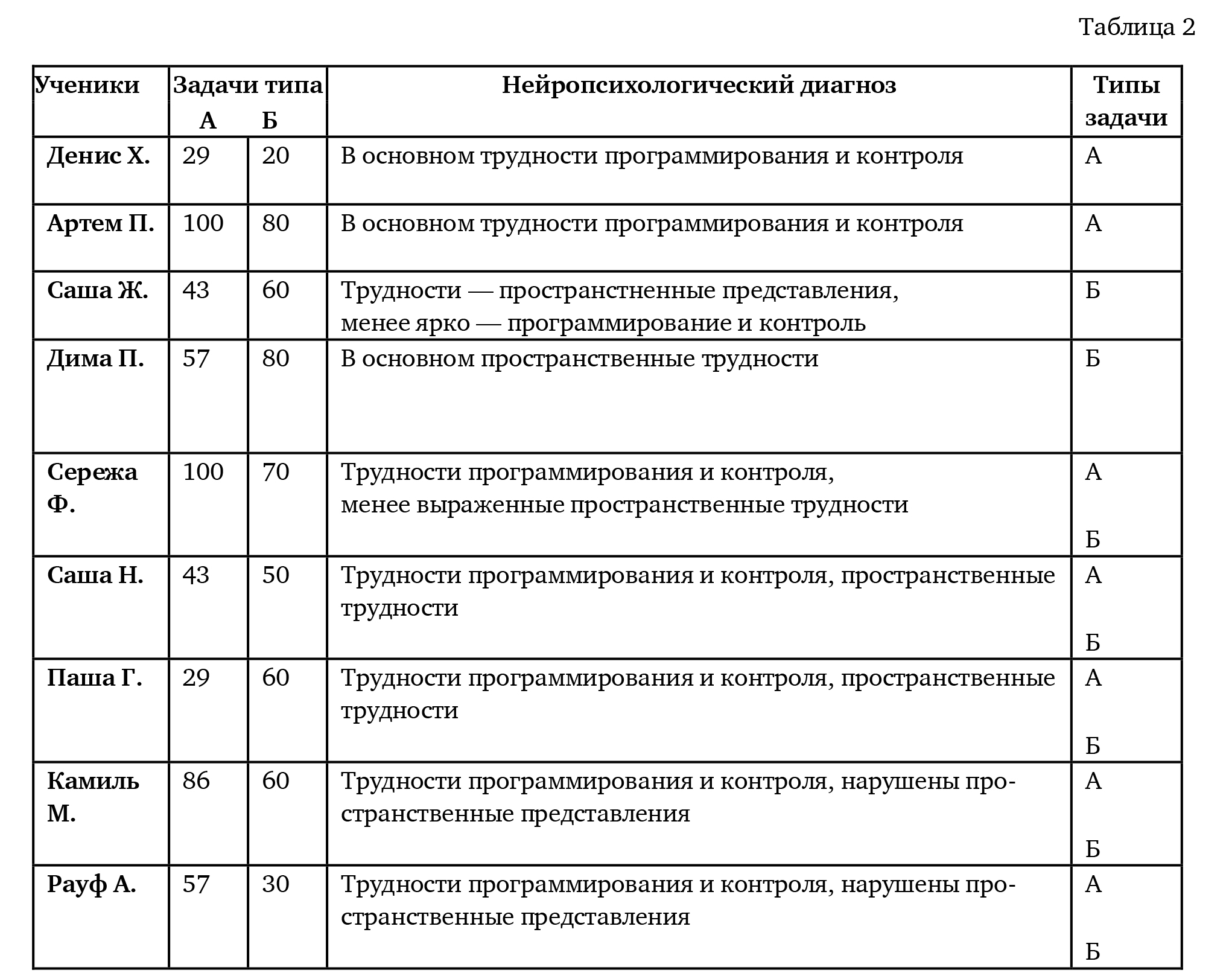
По данным табл. 2 видно, что существует связь между результатами решения задач и типом нейропсихологического диагноза. Дети с трудностями программирования и контроля показывают больше ошибок в задачах типа А, дети с пространственными трудностями и трудностями ориентации в логико-грамматических конструкциях хуже справляются с задачами типа Б. Однако многие дети испытывают трудности при решении задач обоих типов.
Проверка третьей гипотезы
Наблюдая за решением задач нашими испытуемыми, мы предположили, что трудности в решении простых арифметических задач могут быть связаны у них с несформированностью обратимых операций, что можно обнаружить с помощью тестов Ж. Пиаже. Поэтому мы решили проверить выполнение логических заданий (по Ж. Пиаже) у детей, испытывающих трудности обучения математике и имеющих определенный нейропсихологический диагноз.
Исследование проводилось в экспериментальной и контрольной группах. Детям предъявлялись четыре задачи Ж. Пиаже.
Задача 1. «Два пути». Поезд экспериментатора идет по зигзагообразной дороге, а поезд ребенка — по прямой. Поезд ребенка должен пройти такой же длины путь, как путь экспериментатора.
Задача 2. «Бутылки». Ребенка просят нарисовать уровень жидкости в бутылках, по-разному повернутых по отношению к поверхности стола.
Задача 3. «Улитка». Ребенка просят нарисовать, как будет выглядеть улитка, которая, перемещаясь по кругу, достигает положения, противоположного исходному.
Задача 4. «Перчатка». Ребенка просят нарисовать перчатку, которую переворачивают на плоскости слева направо, сверху вниз, справа налево.
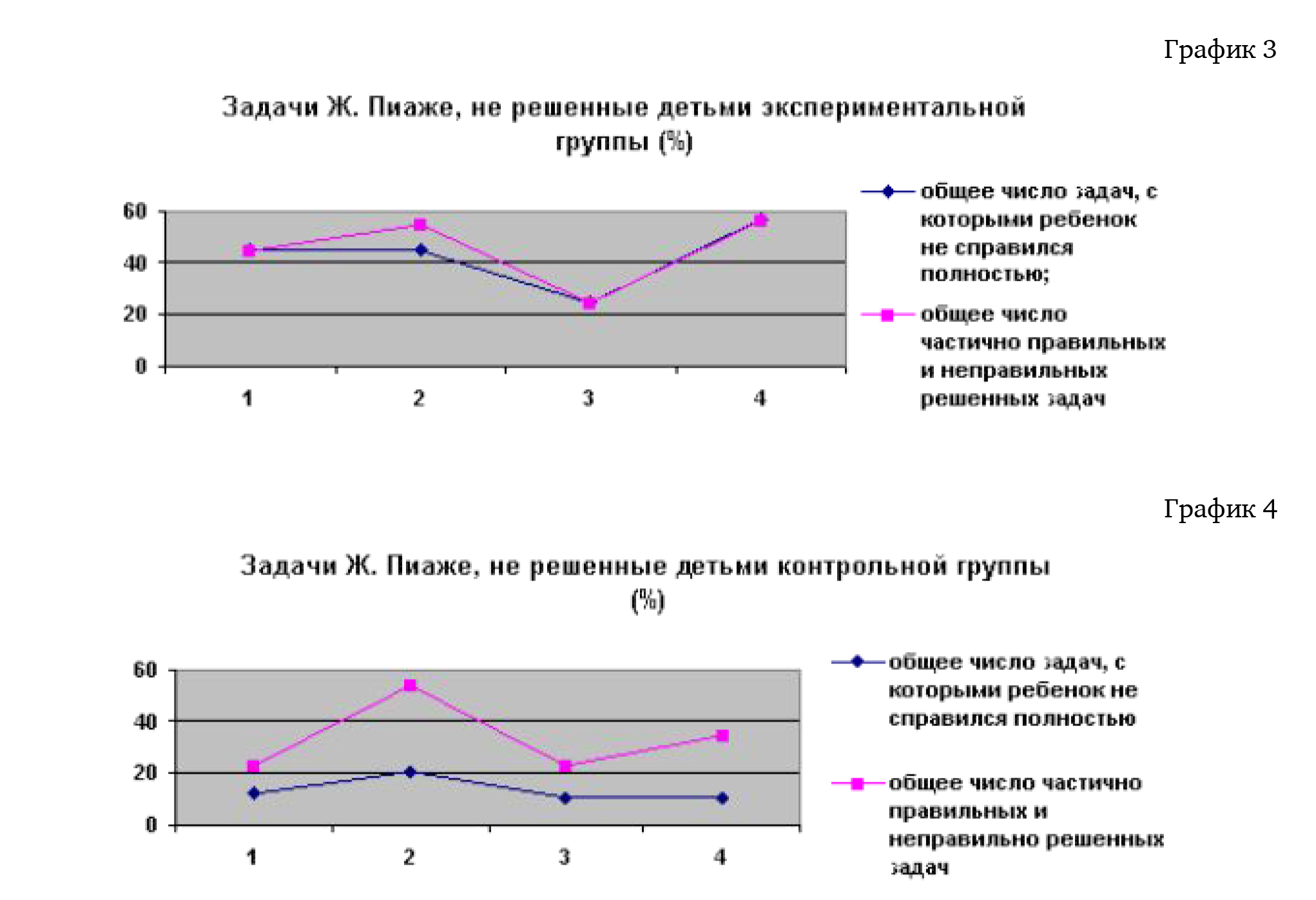
Задания предлагались детям экспериментальной и контрольной групп. Результаты представлены на графиках 3 (экспериментальная группа) и 4 (контрольная группа).
При сравнительном анализе данных видно, что количество неверных решений значительно больше в экспериментальной группе. У детей контрольной группы заметна тенденция к правильному выполнению всех заданий (см. пространство между линиями 1 и 2). В экспериментальной группе задачи выполнялись в основном полностью неверно и подобный разрыв не наблюдается. Можно предположить, что этот разрыв фиксирует зону ближайшего развития детей контрольной группы. Зона ближайшего развития детей экспериментальной группы значительно уже.
Проверка четвертой гипотезы. Анализ индивидуального случая
Для детального изучения причин хронической неуспеваемости по математике был проведен подробный анализ индивидуального случая.
Для проверки были выделены следующие параметры: возможные отставания в интеллектуальном развитии; отсутствие умения сокращать процесс выполнения математического действия и составлять краткие схемы к условиям задач; несформированность пространственных представлений.
Данные из анамнеза. Федор П., 10 лет, второй ребенок из многодетной семьи. В семье четверо детей. До школы развитие соответствовало норме. Жалобы мамы связаны только с плохой успеваемостью сына в школе. До середины II класса мальчик писал левой рукой, затем по настоянию школьного психолога был переучен писать правой. Уроки все школьные годы выполняет вместе с мамой, так как она считает, что без нее ребенок не справляется с заданиями.
Первое обследование уровня математических знаний (возраст 9;1, учится в III классе, 1998). Не умеет делить и вычитать. Умножение выполняет правильно в пределах тех значений таблицы умножения, которые знает. Всю таблицу умножения не может выучить второй год. Причем умножение в порядке возрастания помнит, но не умеет пользоваться этими знаниями. Практически не способен совершать обратные операции, поэтому не может выполнить операцию деления даже в тех случаях, когда знает соответствующую строчку таблицы умножения. На просьбу последовательно вычитать по 7 из 50 отвечает молчанием. При выяснении, в чем состоит трудность, говорит, что запутывается, когда начинает вычитать по единице. Еще сложнее становится вычитание при переходе через десяток. После второго вычитания следующие 7 единиц он вдруг начинает прибавлять.
Очевидно, у ребенка плохо сформировано представление о числе, действии с ним, разрядах и пространственном расположении чисел на числовой прямой.
Второе обследование. С момента проведения предыдущей проверки уровня математических знаний прошел год. Мальчик учится в V классе, его возраст — 10;1. По сравнению с прошлым годом значительно улучшилось качество выполнения математических операций (сложение, вычитание, переход через десяток умеет выполнять без ошибок). Простые и косвенные задачи в одно действие быстро и правильно решает в уме. Однако, несмотря на то, что в процессе обследования использовались задачи из учебника I класса, мальчик мог их решить не все.
Проанализируем состав задач и сделанные ребенком ошибки.
Давались следующие задачи: задачи прямые и косвенные, с переходом через десяток; задачи, используемые в нейропсихологическом анализе; задачи-ловушки, выявляющие умение видеть проблемную ситуацию и анализировать соответствие условий и требований задачи[6, № 15—21]; проверочные задачи[6, № 23—26, 7].
Рассмотрим приемы и сделанные ребенком ошибки:
- При решении задачи «Посчитай общий возраст своей семьи» мальчик долго подсчитывал последовательно все действия, не пытаясь сократить вычисления.
- При решении «конфликтной» задачи «Если 3 карандаша стоят 5 рублей, то сколько стоят 24 карандаша?» ребенок сначала не смог ответить на этот вопрос. По просьбе экспериментатора изобразить ситуацию задачи на рисунке он нарисовал все 24 карандаша. При этом в изображении он не использовал символическое замещение, например, в виде палочки, а вырисовывал каждый карандаш. Естественно, такой развернутой процесс не может протекать сокращенно во внутреннем плане, что значительно удлиняет и усложняет решение.
- Задачи с грамматической конструкцией «на сколько», «во сколько раз» вызывают непонимание: что надо делать? Делить или вычитать, умножать или складывать? Ребенок знает об этих своих ошибках и постоянно говорит себе вслух: «На сколько — это умножить?» Он сомневается и не спешит совершать действие, ждет помощи экспериментатора.
- Федя не смог решить «конфликтную» задачу «От проволоки сначала отрезали 12 см, потом — 7 см. На сколько сантиметров уменьшилась длина проволоки?» Он пытался сложить куски отрезанной проволоки, но тут же поправлялся: «Нет, это не то. Так я получу длину, когда она была еще не отрезанной».
Обращает внимание чрезвычайная развернутость операций, вычислительные операции не доводятся до автоматизма. Из литературы известно, что быстрое свертывание процесса математического рассуждения отличает математически одаренных детей[8]. У детей с трудностями обучения математике не вырабатываются автоматизмы, которые ускоряют процесс решения задач, особенно типовых.
Анализируя трудности освоения начального курса математики у Феди, мы провели комплексное психологическое и нейропсихологическое обследование, необходимое для исключения умственной отсталости и педагогической запущенности.
Результаты обследования интеллектуальной сферы
- Тест Векслера. Общий результат тестирования соответствует норме — 114 баллов. Средние результаты вербальных и невербальных субтестов одинаковы — по 113 баллов. Однако выявлен очень существенный разброс данных по различным субтестам: от низшей границы нормы — 7 баллов в арифметическом субтесте до 15 баллов в словарном и 16 баллов в субтесте «понятливость» — это выше средней нормы. Аналогичная картина наблюдалась и в невербальных субтестах: шифровка — 7 баллов, недостающие детали — 14 баллов, кубики Кооса — 17 баллов.
- Цветные матрицы Равена. Решены все задачи, кроме последней, что для этого возраста составляет P=95%. После проведения стандартной процедуры последнее задание было решено с помощью психолога, указавшего на определенную логическую закономерность.
- Пробы Ж. Пиаже. Были проведены пробы на сохранение количества жидкости, трансформацию и пространственную ориентацию, а также пробы на запоминание: сериация и сохранение правильного количества спичек. Все пробы выполнены верно. Можно считать, что произошел устойчивый переход на уровень конкретных операций.
- Рисуночные методики определения интеллекта. Рисунок человека по методике Гудинаф — Харрис соответствует IQ=111, а по методике «Дом, за которым растет дерево» мальчик находится на стадии зрительного реализма.
- Методика Бендер. При подсчете баллов по Свинярскому — Цессельскому ребенок набрал 30 баллов при средней норме 22 балла и при диапазоне 18 — 26. Результаты свидетельствуют о трудностях сенсомоторной координации и, возможно, планирования (рисунки хаотично расположены на листе). Однако в рисунках нет грубых деформаций, все ошибки в основном связаны с неточностями изображения.
По результатам проведенного обследования развитие ребенка можно считать соответствующим возрастной норме, с некоторым отставанием в сфере сенсомоторной координации.
Для проверки одной из гипотез о возможных нейропсихологических трудностях мальчик был обследован нейропсихологом и невропатологом. Невропатолог обнаружил нарушение регуляции тонуса мышц, вегетативные нарушения, высокие рефлексы (склонность к невротизации) и множество признаков нарушений по «лобному» типу.
Заключение: в неврологическом статусе на первый план выходят признаки функциональной недостаточности нижнестволовых структур и передних отделов полушарий головного мозга.
Нейропсихологическое обследование проводилось по стандартной схеме обследования детей 6—8 лет. Оно построено на основе батареи проб А. Р. Лурии. Схема нейропсихологического обследования адаптирована и апробирована на детском контингенте сотрудниками Лаборатории нейропсихологии МГУ[2]. Обследование ребенка проводила нейропсихолог Комплекса социальной помощи детям и подросткам Е. А. Юртова.
Были проведены пробы на проверку зрелости функций планирования и контроля произвольных действий: реципрокная координация в норме; динамический праксис — при выполнении второй программы тенденция к ее упрощению, заучивание со счетом; реакция выбора — сбивается при ломке стереотипов, самокоррекция; серийная организация движений (графическая проба) — снижен контроль, не выполняет инструкцию, так как постоянно отрывает ручку от бумаги, тенденции к персеверации с самокоррекцией.
Зрительный гнозис при опознании перечеркнутых и реалистических изображений — семантические замены (балалайка — гусли, чемодан — сундук, чайник — утюг).
Зрительная память. Кривая заучивания: 4 5 5 (из 5 фигур). Упрощение элементов.
Слухоречевая память. Снижение объема запоминания после интерференции. Запомнил 5 из 6 слов. После интерференции — 4.
Зрительно-пространственные представления — в норме.
Фонематический слух — в норме. Слухомоторная координация — в норме.
Понимание логико-грамматических конструкций нарушено (из 13 конструкций понял неправильно 4).
Выполнение интеллектуальных проб в норме.
Заключение нейропсихолога: на первый план выступает импульсивность при выполнении большинства заданий. Незрелость функциональных структур блока программирования и контроля произвольных действий. Легкое отставание в развитии зрительно-вербальных функций. Недостаточно сформировано понимание логико-грамматических конструкций.
Комплексное обследование ребенка выявило, что по уровню психического развития он соответствует возрастной норме, однако в пределах возрастной нормы отмечены отклонения в развитии квазипространственных функций, сенсомоторных координации, импульсивность в операциях программирования и контроля. Именно эти особенности ВПФ требуют прицельной коррекционной работы. Третье обследование для выявления трудностей в усвоении математики происходило спустя один год. На этот раз целью проверки было понимание ребенком различных вариантов схематизации простых арифметических задач. Ребенок успешно составил схемы к задачам, используя отрезки различной длины.
В решении и схематизации простых арифметических задач заметен прогресс. Однако сокращение действия у этого ребенка еще не достигло уровня простой формулы. Это выяснилось, когда ему были предложены другие варианты схематизации этих же задач, составленные экспериментатором. Среди схем наряду с правильными были и ошибочные.
Ребенка просили выбрать схемы, соответствующие содержанию задачи. С заданиями, представленными в такой форме, ребенок не смог справиться. Он выбирал верно только те варианты схем, которые были аналогичны его собственным. Схемы, которые он научился составлять на уроке, он не мог перенести на другой иллюстративный материал. Таким образом, было выявлено, что у данного ребенка нет смыслового понимания отношений, заданных в схеме условия задачи. (Те же самые схемы, предложенные другому ученику того же возраста, успешно усваивающему школьную программу по математике, не вызвали никаких трудностей.)
Заключение
В работе проанализированы трудности в усвоении начального курса математики, возникавшие у детей младшего школьного возраста. Показано, что низкий уровень усвоения математических знаний не является прямым и единственным следствием грубой педагогической запущенности, умственной отсталости или сложности учебной программы.
Получили подтверждение гипотезы о том, что вербальная форма предъявления арифметических задач (тип А — задачи со сложной формулировкой условий, требующие составления программы последовательных действий; тип Б — задачи, в формулировке которых использованы сложные логико-грамматические конструкции) служит причиной ошибок в их решении.
Однако, как известно из теории Ж. Пиаже, для полноценного усвоения математики необходимо формирование умственных действий, обладающих свойством обратимости. Как показало исследование, дети, испытывающие трудности в усвоении математики, находятся на переходной стадии от дооперационального к конкретно-операциональному мышлению.
Сложности в осуществлении умственных операций могут быть скрытой, внутренней, причиной затруднений в понимании логической формы словесной задачи. Дети, имеющие нейропсихологический диагноз, отличаются от детей общеобразовательной школы (условная норма) узостью зоны ближайшего развития по задачам Ж. Пиаже.
Основу трудностей обучения могут составлять индивидуальные особенности формирования высших психических функций, обусловленные незрелостью определенных функциональных блоков нейропсихической организации головного мозга. Проанализированные в работе сложности сокращения действий при решении арифметических задач могут быть следствием диспропорционального развития высших психических функций.
Для выявления причин неуспеваемости необходим детальный индивидуальный анализ каждого конкретного случая, чтобы выявить слабое звено в познавательном развитии ребенка. Только на этой основе можно разрабатывать программу психокоррекционной работы.
При построении коррекционного обучения математическим понятиям и действиям необходимо учитывать не только содержание программы и методики ее преподавания в классно-урочной системе, но и индивидуальные возможности восприятия и анализа учебного материала конкретным ребенком, которые можно выявить на основе нейропсихологического и возрастнопсихологического обследования.