Учебный процесс в математическом образовании: выготскианский подход

Introduction

The paper aims to point out the recent applications of the semiotic mediation theory, based on Vygostky's contribution. One of the main purposes of the teacher in the kindergarten level is to promote the construction of mathematical meanings in a fun way, according to the age of the children involved. In this paper it is stated that the teachers can use tools as instruments of semiotic mediation . The link between this theory and the use of tools as artifacts in kindergarten is shown in the following sections according to the Research Group of Modena and Reggio Emilia leaded by Prof. Bartolini-Bussi (Bartolini-Bussi, 2010). Since the '80s, the Research Group in collaboration with the Core Program in History and Mathematics Education of the University of Modena and Reggio Emilia, has leaded educational paths aimed at introducing into teaching activities the use of structured materials carried out by mathematicians, from old to modern times, such as abacus. The historical dimension has been linked with the manipulative and the visual dimension of the materials, in order to facilitate the learning process of mathematical concepts and theories.

The paper summarizes the connection between tools and language by showing the interplay of signs and symbols, as mediators in the development of the cognitive functions, in particular retracing Sfard and her notion of commognition (2008).

Secondly it focuses on the notion of artifacts according to the historical and epistemological perspective, trying to investigate the instrumental genesis as one of the major contribution in the cognitive ergonomy, assuming that this concept could be expanded to the mathematical education.

After introducing the notions of artifacts and signs in the theoretical framework of semiotic mediation, it is highlighted the distinction between the mathematical machines, arithmetical and geometrical according to Bartolini-Bussi' theory, focusing on the relationship between the theoretical framework of the semiotic mediation and the didactical cycle.

1.    Tools and Language: A dualistic view to develop cognition

The process of our development through evolution can be followed or mapped by looking at the use of tools. Writing could be considered a "source of specific thought schema" (McLuhan, 1962; Ong, 1967 in Bartolini-Bussi & Mariotti, 2008) it's proof that, from the beginning of human existence, the tools (language included) create a representative form of human thoughts as in the transition from the oral to the written language.

Retracing the works of Vygostky, it is important to emphasize the social aspect of knowledge as described in Thought and Language (1986), in which the development of higher mental functions results from the use of language in social interaction. Language in all its forms becomes the first tool of concepts mediation that influences thought itself.

In particular, a contemporary researcher, Anna Sfard, in her Thinking as Communicating (2008), leads an analysis of the Vygostkian language theory, thus reaching the theory of commognition, a mix of communication and cognition, that highlights the close connection between thought and language.

Vygostky considers language as a social cultural production and as a product of thought in the historical-cultural evolution. Conceived as a system of cultural mediation of cognitive functions, language enables human to act in an appropriate and effective way in the cultural context. Cognitive functions and mental categories are both mediated by language and signs, having a historical and conventional meaning. Our language does not simply describe what exists, but is responsible for what we think is real (Ibidem). In this sense it is possible to speak, according to Sfard, of commognition. Language is a symbolic expression, not only in oral and written form, but also figuratively. Signs convey social meanings and therefore become the first tool of mediation.

2.    The notion of artifacts in the historical-epistemological approach

The historical-epistemological point of view considers that artifacts are polysemic because they have assumed different functions and meanings according to the context of use: practical and/or theoretical.

The word artifact refers to something created by men for a specific reason (Fiorani et al., 2011). All the material objects are artifacts or tools modeled by human activities and require a project, a purpose, with an embodied intelligence and a creative activity.

Some important features, such as the size of the object and the idea of the project that supports the artifacts with a specific aim, are shown in a more complex concept, introduced by the definition of Wartofsky (1979) who, in Perception, representation and the forms of action: towards an historical epistemology, proposes a three-level hierarchy of artifacts: primary, secondary and tertiary artifacts.

The primary artifacts, are a fundamental tool for a possible mediation between the subject and the surrounding reality. These kinds of tools are designed for a practical action, such as the pen to write, the compass to draw a circle or the abacus for counting. These types of primary artifacts make the extension of the human potentiality possible, playing the role of cultural prosthetic for the interaction with the reality.

The secondary artifacts are the primary artifacts to the next level. In fact they imply a greater processing of primary artifacts, making it possible to interact, use, modify and process the primary artifacts. For example, the abacus has been widely used in the ancient world as a calculation tool within the commercial activities. The use of this tool is no longer just linked to the practical action it was created for (counting activities directly on the artifact) but is now linked to its modes of action. This second type of artifact offers the symbolic dimension that allows us to use the primary artifacts. Secondary artifacts are therefore representations of these modes of action.

The tertiary artifacts are the further elaboration of the secondary artifacts, thus reaching the meta-cognitive dimension. This latter type leads to a more independent level of schemes, logical perspectives and models that Wartofsky defines as 'imagined worlds' autonomous and independent from the practical activity. Tertiary artifacts are no longer linked to the practical action of the reality, they exist as a separate world: the theoretical one.

In general, the understanding of the concept of artifact is the base to consider the human dimension in its historical and environmental context: think of the cultures of the past who can tell of past experiences and behavior patterns through the tools they used, the works and artistic rituals. Artifacts condense the signs of their cultural-historical development in which they are designed (Ligorio, 2003) and are progressively recreated through their own use, that continuously change and evolve themselves.

The artifact is, in short, a mediation-tool between the subject and the external dimension of the reality. Norman has clearly described the concept expressed by the word artifacts in the title of his book Things that make us smart (1993). This refers to the double nature of the cognitive artifacts: on one hand they are created as tools (external process), on the other hand they made us smart by improving our logical reasoning and cognitive activities (internal process).

3.    The instrumental approach

The background cultural framework of this field of studies is linked to the cognitive ergonomy perspective of Rabardel (1995a-b). He starts to investigate the interaction between human and technological tools and uses Vygostky' studies as a starting point. It goes without saying that technological tools have been a great impact on cognitive processes by introducing new ways of thinking and communicating to humans; this field of studies refers to humans and technologies (mainly referring to machines used in industrial companies) but it is important to bring this approach into the field of education.

In particular, artifact and instrument are different concepts for the author:

— The artifact can be a material or symbolic object, but it is often developed with a particular goal, therefore it already has knowledge within it.

— The instrument is based solely on the psychological character and begins when the development occurs.

This distinction introduced by Rabardel concerns the process named (by him) instrumental genesis, consisting in the instrumentalisation of an artifact and in the instrumentation of it:

— The instrumentalisation is the discovering of the elements and qualities of the tools.

— The instrumentation is the knowing of all the potentialities and applications of the tools linked to the utilization schemes.

The theorization of Rabardel stresses that the use of tools always triggers a mechanism in cognitive structures, leading them to build and organize new ones. This process is permitted by the social interaction. The sharing activity in a community of practices help us to shape and re-organize cognitive structures through the coac­tions of social schemes and individual utilization schemes. These are both linked together.

In particular, according to Rabardel's instrumental genesis theorization, the use of a specific tool in the teaching and learning of mathematics in a class, as a community of practice, could help students to enhance their learning process. In the paragraph titled The case of a giant abacus it is shown how the instrumental genesis leads the teacher to design specific activities in order to enhance the mathematical discussion in the kindergarten level.

4.    The concept of Mediation by Vygostky

Vygostky stated that the use of tools is essential in the learning process therefore creating the base to study the use of artifacts in the field of education. The revolution introduced by Vygostky, during the 1930s, breaks the chain introduced and theorized by the behaviorism perspective (the direct link between subject and object in the cognitive processes), by introducing the tool as an element, enhancing the mediating activity of the cognitive process between subjects and objects: "like words, tools and nonverbal signs provide learners with ways to become more efficient in their adaptive and problem-solving efforts". (Vygostky, 1978, p. 127).

The field in which Vygostky matures this reflection is a period of cultural fervor, after the October Revolution (1929) in Russia. The idea of rebuilding a better society and the liberation of the schemes of the past, a vibrant active driving force to create ideas and suggestions that has had a broad impact on the world and significantly influenced many contemporary perspectives.

In particular, he has made a great contribution by noting the complexity of human cognitive development. Generally interconnected with other cultural aspects such as biological, historical, instrumental and socio­cultural, that make up the complexity of human thoughts (Vygotsky,1987).

This Russian author's studies focus on a particular development of higher mental functions (specifically thought and language) as evidence that they are deeply influenced by social and cultural conditions, in which an individual is experiencing the world. This brings him to formulate the general genetic law of cultural development that consists of any higher mental function as appearing twice in the child's psychological development: the first on the social (inter-psychological) and the other on the psychological level (intra-psychological). He states that:

"[A]ny function in the child's cultural development appears twice, or on two planes. First it appears on the social plane, and then on the psychological plane. First it appears between people as an inter-psychological category, and then within the child as an intra-psychological category. This is equally true with regard to voluntary attention, logical memory, the formation of concepts, and the development of volition [...] it goes without saying that internalization transforms the process itself and changes its structure and functions. Social relations or relations among people genetically underlie all higher functions and their relationships" (Vygostky, 1981, p. 163).

Vygostky's thought starts to take into account the centrality of the cultural dimension, the social interaction with peers and adults as important factors, not insignificant, in a child's development and these notions will have an ever increasing influence in the contemporary studies and research.

In the field of education, the distinction between the concepts 'spontaneous' and 'scientific' introduced by Vygostky are very important. Spontaneous concepts are linked to everyday activities and learned in daily situations, whilst scientific concepts need more specific settings and a systematical activity focused on reflection, exploitation, formulation and reconsideration (Wells, 1994). These activities that lead to the construction of scientific concepts in children are generally carried out in a school setting and require an instructional style predetermined by the teachers (the definition of the Vygostkian zone of proximal development, ZPD, as the distance between the actual and the potential level of development, is crucial in the field of education).

As stated before, according to the general genetic law of cultural development (Vygostky, 1981), the cognitive development in children is lead by the social interactions with peers and adults. The development of higher mental functions is tied to the formal and informal activities experienced in the cultural context.

However, it is also important to recall, according to Wells, that tools have a central role when he states that: "central to Vygotsky's 'genetic approach to the explanation of both socio-historical and individual development is the recognition of the pivotal role of tools" (Wells, 1994, p. 3). Thus we can say that the first appearance of a spontaneous concept is often related to the child's interaction with an object, while the birth of the scientific concept is through a mediation. In the first case there is a natural object related to the concept, while in the second case it travels in the opposite direction (Vygostky, 1987). The learning of mathematics is related to concepts that may be different and also quite far from those related to human immediate experience (Sfard, 1991). Obviously this does not mean that the learning of scientific concepts can disengage from the experience (Bagni, 2006).

The role that experience plays, at least initially, is fundamental and in many ways is seen in the move from scientific concepts to those that are abstract. Therefore, the use of tools as mediators facilitates the learning of mathematical concepts by reducing the distance between the spontaneous and the scientific concept.

The main educational function of tools-mediators is to support the acquisition of new knowledge from a field of a family experience to a new one. As well as through the exploration of the elements of the tools (in a specific instructional setting) children are going to perceive the concepts they actually have interplaying and interchanging them within their new ones.

In many cases the choice of a tool-mediator is the result of a not critical choice lead by the teacher and it is an integral part of any educational process.

Starting from the notion of semiotic mediation, in which cognitive development is driven both by social interactions and by use of signs and tools. In recent years, the Research Group of Modena-Reggio Emilia in Mathematical Education has led teaching experiments designed to analyze the role of tools in the mathematical learning process (Bartolini-Bussi & Mariotti, 1999—2011).

5.    Artifacts and Signs in the theoretical framework of semiotic mediation

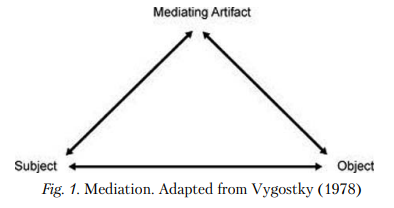
The idea of artifact is general (Vygostky, 1997), but the use of artifacts is essential to the learning process of mathematics. In fact, there is not a direct link of mathematical knowledge to practice, but the use of tools mediates the constructive learning process (Duval, 1993, 2005). In the theoretical framework of semiotic mediation artifact (Fig. 1) means "a material part of the environment intentionally modified by man for use with specific intent" (Bartolini-Bussi & Boni, 2011, p. IV). In this section we intend to use the term artifact, as previously discussed in section 2.

The research conducted as teaching experiments is based on the use of artifacts in the classroom as tools of semiotic mediation for the teachers and it consists of three main stages:

1.   Activities with artifacts. In this stage the teacher gives a task with the artifact to children. They can discover the artifact, its structure and its material components, during the task activity.

2.    Individual production of signs. After the first stage, children are engaged in several activities, centered on semiotic processes (production of signs in drawing, writing and other activities), that referred to the previous activities in which they were involved.

3.    Collective production of signs. The teacher leads the students in a collective discussion about the previous activities made up with the artifact. This stage is very important because children can speak about their thoughts and experiences and the teacher can start a mathematical discussion. The teacher can lead the students towards the construction of mathematical meanings that is the main aim of the didactical cycle.

These studies have shown a gradual emergence of relations of meaning between artifacts and mathematical symbols, signs or between closely related to the activity with the artifact to signs commonly shared by the community. In this sense Bartolini-Bussi and colleagues considered the notion of semiotic chain, linked to the use of the artifact, related to Wartofsky and Rabardel theorization, and it can be expressed in three categories of signs in relation to each other:

1.    Artifact-signs: are derived from the actual artifact, the way it is used or a part of the artifact. The signs from the artifact are different for each student or if the students are working in pairs. Artifacts signs come in all different types and forms, such as hand gestures, drawings, verbal or non verbal. They are related to the action with the artifact. As basic elements of the semiotic process, they express personal meanings implicit related to how the subject interprets the activity with the artifact. They are also the signs located that they are related to the usage context of the artifact.

2.    Pivot-sign: are the actions used with the artifacts signs to obtain the goal. These steps and action polysemic are related to the activity with the artifact, but also to natural language than the mathematical one. They are an early form of generalization and learning in the cycle, used in the classroom by the teacher to create relationship with the mathematical language of the community.

3.    Mathematics Sign: These signs are used in classroom settings and refer to the formal language of mathematics. They are pre-orchestrated by a mathematical community that is based upon cultural heritage. Such different signs can be traced in the evolution of student learning bringing out the chain of semiotic meanings of the activity with the artifact and the mathematical signs, goal of mathematical education.

In this process it is essential that the teacher be a mediator between artifacts and pupils. In fact, the teacher manages the discussion of mathematical tasks, with particular focus on the pivot-signs to lead children to mathematical signs.

The different signs in fact, generate a chain of semiotic meanings in relation to which the external reference gradually disappears and yet it is held there by a chain of meanings that gradually shifts: from highly contextualized signs, closely related to the use of artifacts, towards mathematical signs, which are the target of the teaching/learning process.

The pivot-signs are intermediate between artifact and the mathematical signs. Pivot-signs express the first detachment by the artifact while maintaining a link with it as not to lose their meaning.

In the theoretical framework of Bartolini-Bussi and colleagues the goal of the teacher's action is to recognize the various signs that emerging in the activity with the use of the artifact and know how to manage a group discussion toward the mathematical signs socially negotiated and shared in the mathematics community. The theoretical framework of semiotic mediation therefore considers the artifacts as semiotic mediators, although the passage from the exclusive use of the instrument to the construction of mathematical meanings is still linked to the action of the teacher: tools are an instrument in classroom activities and teacher can use them as a crucial element in the construction of knowledge.

6.    Mathematical machines in teaching/learning processes

The Research Group of Modena-Reggio Emilia over the years has created a collection of historical mathematical machines (Bartolini-Bussi & Quattrocchi, 1992; Bartolini-Bussi & Maschietto, 2006, Maschietto & Bartolini-Bussi, 2011)) made up in different schools and in different provinces, that can be categorized in two different types: arithmetical machines and geometrical machines:

1.    The arithmetical machines are tools that allow us to operate with numbers. They were made up to represent numbers or for calculating algorithms (e. g. abaci, mechanical calculators, Pascaline). For example, the Pascaline (Fig. 2) were originally invented by Pascal, in 1642, and has been recently rebuilt and named Pascaline 0+1 (Fig. 3) to allow its use in schools. Children could use the Pascaline for the positional notation of numbers and the algorithms (Bartolini-Bussi, 2011).

2.   The geometrical machines are tools that force the geometry of a point or a figure to move, or to be processed in accordance with predetermined mathematical laws (curvigrafi, pantographs, compasses, perspectographs).

We're going to consider the arithmetical machines in this paper, in particular, in the next section we take, as a case study, the giant abacus (Fig. 4) in a path of action­research conducted in some schools, at kindergarten level, of Northern Italy.

7.    The case of a giant abacus

To better understand the relationship between the theoretical framework of the semiotic mediation theory explained in section 5, along with the didactical cycle implemented by the teacher, it seems appropriate to briefly bring back a sample.

The path that follows is taken from the action­research project in the schools of Modena (Italy) led by Professor Bartolini-Bussi together with the kindergarten teachers of the schools and 20 classes with children aged 3 to 5 years (Bartolini-Bussi & Boni, 2011).

The project focuses on numeracy.

The participating schools were given a giant unassem­bled abacus consisting of 40 balls, in order to allow the registration of children present and count the days of the month. The task is designed to promote a discussion about numeracy. Children were asked to make an abacus and, during the activity, they were proposed to discuss about numeracy, starting with the discovery of the artifact.

In particular, there are three salient points that have guided the experimental path:

1.    The discussion orchestrated by the teacher, in small and large group, to enable the verbal interaction in the community of learners.

2.    The use of different systems of representation (semiotic processes), such as gestural and graphic, as well as verbal.

3.    The use of a historical artifact (the giant abacus) to ensure a cultural consistent first approach to counting activities.

But how is possible to interplay the two aspects? Namely the mathematical knowledge and the knowledge expressed by the children through the use of the artifact. 

To better explain it is useful to analyze some questions that connect the theoretical framework of semiotic mediation through action and education that can facilitate the work of the teacher by leading her action (Bartolini-Bussi, 2011).

The 'good questions' are the following:

1.   What is it?

2.    How is it done?

3.    What does it do?

4.    Why does it do this?

5.    What would happen if..?

The five questions are aimed at children, after a task activity with a specific artifact, the abacus in this case. Now, a more extensive description of the questions, related to artifact on one hand and to the children's learning process on the other hand, focusing the discussion on teacher's actions, will be presented.

What is it?

The question What is it? is placed at the moment when the children discover the artifact-abacus. In the experiment we are referring to, the abacus is presented unassembled and the curiosity and imagination of children are widely ranged in speculation of various kinds.

In this phase the teacher leaves the children free to say whatever comes into their mind, even encourages them to question and to relate this experience with others who may have already done.

The child must be able to feel free to talk about themselves in relation to the object that is discovered and it is important that at this time the teacher does not immediately give a delivery, because the child would otherwise be required to meet the demands of the teacher rather than turn his attention to the narration of what is being experienced.

And then the narrative aspect of nature must be apparent at this time, and is the voice of the 'narrator' who prevails as free space in which children can say what they want, as it feels. But at this stage the teacher can teach the conventional name. For example, it may be that a child already knows it and says the name.

How is it done?

The question How is it done? is a gradual revival going from what it is to attempting to describe parts of the artifact. This brings the voice of the 'builder' and the teacher guides the discussion and then verbally requests a graphic representation of the artifact. The description of the spatial aspect of the artifact, the identification of components, name them correctly, describe the spatial relationships between the parties (e. g. There are legs that are used to fit the feet and legs are made of iron and there are balls to make it go back and forth, etc. ..) lead the children to express themselves freely using the language, verbal and graphic, but also gestures, providing their vision of the artifact, introducing them to analyze and problematize the object they face.

The teacher then ask: "What do we need to build another one?", "What should we buy if we want to build an abacus?", "How many balls are there?"

What does it do?

The question What does it do? is oriented to make the children understand the functional aspect of the artifact taken into account and is the voice of the 'user'. For example you can use the abacus to count the children that attend school. It can be used during the attendance or other everyday situations. The teacher can also use it to practice the rhyme of the numbers in counting situations.

Why does it do this?

The question Why does it do this? is to make children discover knowledge embedded in the artifact-abacus. It is no coincidence that the abacus has ten balls: one begins to enter in game theory (voice of 'theory') because it introduces the system of positional notation.

An example that can easily be shown in the class is the game with the 'silly snowman': a teacher who has participated in the trial has created a drama (comedy in three acts with children of 5 years) in which a puppet fool committing all the mistakes that children often make when counting and the children are called to correct it. In addition to seeing how the theory of the numbering may enter an activity with the abacus, it is important to note the emotional aspect that guides the action of the teacher, in this case, since it is easier to correct a puppet that is wrong rather than a child.

What would happen if...?

The question of What would happen if...? brings into play the voice of a 'problem solver'.

Another example is that of a school where the children had decided to use the abacus to set the table and count how many children at each table, then bringing them back to the abacus. The game worked very well since there were four tables in the section that corresponded to the four files, so the children writing down how many children at each table. But then one day the teacher brought another table.

With the abacus the fifth table is no longer good and the children took the small cubes and put them on the ground and came up with a fifth row that was not there.

The children did what in studies of cognitive ergonomy is called instrumentation of the artifact, i.e. the change of the artifact to the purpose, which in this case occurred directly.

One can pose the problem in an indirect and gradual way to the children by asking: "but if we go in the class of three years and there are six tables how can we use our abacus to record how many children are in each table?"

Conclusion

The didactical cycle consists of several steps and focuses on the interaction between artifact and child. The child uses the artifacts in his own way and produces the proposed signs. These signs are managed by the teacher and we want to emphasize this pattern at the base of the artifacts: "Thus any artifact will be referred to as tool of semiotic mediation as long as it is (or it is conceived to be) intentionally used by the teacher to mediate a mathematical content through a designed didactical intervention" (Bartolini-Bussi & Mariotti, 1999, p. 754).

The use of tools in the mathematical learning process, through the children' social interaction, enhances the mediating activity of the cognitive process, as Vygostky realised (1978).

Then, what is the task of a teacher? First of all, the teacher is called to expand the semiotic potential of the artifact. She must first understand the knowledge embedded in the artifact and analyze its relation to the of mathematical knowledge that she wants to teach. Secondly, the teacher must then manage the operation of the artifact; that is figuring out how it works what it offers its pupils according to the analysis that has previously carried out previously.

The abacus creates the framework that is used to outline the task accessible to children (for example to count how many pins are in the gym). From this one can connect the knowledge accessible to the children with the knowledge (mathematical) accessible to the teacher (according to the notion commognition by Sfard). The ability to put the pins in correspondence with the balls of the abacus: the children then become stable with the sequence of numbers. The teacher must choose the tasks well in order to create a working relationship with mathematical knowledge, objective education, and knowledge expressed by the children (in this case the correspondence).

In conclusion, it is important to highlight the approaches underlined in the paper because the tools always influence the cognitive development and the construction of mathematical meanings for students. It goes without saying that the reflection upon tools as mediators is, or should be, part of the teacher's concerns. The transition from a material object, a tool, to a didactical object (artifact) is carried out by teachers and, as it is said in many cases the choice of a tool­mediator is the result of a spontaneous choice lead by the teacher.

For more effectiveness in class, it would be interesting to link the research on the semiotic potential of tools, as it is conducted by the Research Group of Modena Reggio-Emilia. This would need a more extensive research upon teacher's will and conception about tools-mediators as artifacts, particularly how the teacher uses the chosen tool to teach mathematics as it is shown in the paper Hand-On Maths in Kindergarten (Fiorani, in press). Six teachers and two researchers have developed educational courses, centered upon the didactical cycle, the use of the tool Contafacile and other unstructured materials, as mediators of everyday objects (73 children aged 5 years involved): "children experience different languages and systems of representation; they learn to build objects using mathematical experiences found in everyday life (...). The project involved teacher training, and their comments were recorded during individual interviews at the beginning and end of the project, in which they were asked to reflect on the possibility of realizing the didactical cycle in their lessons" (Ibidem).

This could give us the possibility to rethink the theoretical framework, carried out by the Vygostkian semiotic mediation theory, with the interventions used in the mathematical education.