Введение
Математические понятия представляют собой сложную логико-гносеологическую категорию и, следовательно, процесс овладения обучающимся математическим понятием является непростым, длительным и многогранным. Проблема освоения младшими школьниками математических понятий является одной из важнейших, как в зарубежной, так и в отечественной педагогической психологии. Этому вопросу посвящено немало работ, но он продолжает оставаться актуальным.
В процессе овладения младшим школьником математическим понятием важно выявлять ошибки, которые он допускает. Качественно проведенный анализ ошибок предоставляет педагогам информацию, на основе которой могут быть приняты наиболее эффективные решения по преодолению индивидуальных трудностей обучающихся. С другой стороны, проведенный M. Левином (2018) обзор исследований в области анализа математических ошибок показал, что авторы используют разные классификации и типологии. Многообразие классификаций ошибок дезорганизует педагогов. Так, П. Риккомини (2005) обнаружил, что до 50% учителей не могут диагностировать конкретную ошибку, не различают типовые и случайные ошибки учащихся. Тем не менее в процессе формирования математических понятий работа над ошибками не просто полезна, но и необходима. Р. Эшлок подчеркивает важность не только обнаружения систематических ошибок учащихся, но и выяснения стоящих за ними неправильных представлений [Ashlock, 2010].
Безусловно, данная проблема является значимой для педагогической работы, нацеленной на поддержку осмысленного изучения младшими школьниками математики.
Обзор исследований типологий основных ошибок младших школьников при освоении математических понятий даст возможность обобщить результаты в данной области педагогической психологии и обозначить актуальные направления будущих исследований.
Значение анализа математических ошибок
Анализ ошибок в математике — это область научных исследований в психологии образования, которая имеет давнюю историю.
Одна из первых публикаций, посвященных анализу математических ошибок, принадлежит американскому ученому Х. Радац. Он отметил, что в конце 1970-х годов появился интерес к изучению ошибок в математике, отчасти потому, что процесс индивидуализации и дифференциации обучения математике потребовал четкого понимания конкретных проблемных зон учащихся. Точная диагностика затруднений учащихся позволяет строить эффективное обучение. Х. Радац утверждал, что без понимания причин ошибок невозможно принимать обоснованные решения в обучении математики. При этом утверждалось, что разные учащиеся могут совершать однотипные ошибки в задаче по математике, но при этом иметь разные причины и разные затруднения. Следовательно, с обучающимся необходимо выстраивать разные стратегии по исправлению их трудностей [Radatz, 1979].
Своим исследованием Р. Бораси (R. Borasi) также показал, что точный и оперативный анализ математических ошибок учащихся может предоставлять учителям своевременную информацию, которую можно использовать для корректировки обучения в соответствии с индивидуальными потребностями учащихся.
Также в конце 1970-х годов в образовании стала популярной идея о том, что в процессе изучения математики и естествознания у учащихся могут развиваться ошибочные представления. Этому способствовали авторитетные высказывания Пиаже о том, что дети думают о мире иначе, чем взрослые [Misconceptions Reconceived: A, 1994]. Таким образом, при анализе математических ошибок многие исследователи стали включать такой тип ошибок, как «заблуждения/ошибочные или неверные представления». В образовании стал развиваться конструктивистский подход, согласно которому любое обучение предполагает интерпретацию явлений, ситуаций и событий, включая обучение в классе, с точки зрения имеющихся у учащегося знаний. В рамках этого подхода опровергается утверждение о том, что обучение в школе ребенок начинает «с чистого листа». Даже у начинающего ученика имеются свои представления, на основе которых он может объяснить некоторые математические понятия [diSessa, 1993; diSessa, 2019; Misconceptions Reconceived: A, 1994].
Фундаментальное исследование Р. Эшлока [Ashlock, 2010], посвященное анализу шаблонов ошибок в вычислениях, позволило собрать коллекцию различных типов ошибок, встречающихся у учащихся в процессе изучения математики, призвано помочь учителям выявить распространенные математические ошибки у детей и получить представление о том, почему ребенок мог усвоить неправильный математический алгоритм действия.
Р. Эшлок дифференцировал неосторожные ошибки, которые мы все совершаем, от неправильных представлений о математических идеях и процедурах, которые приводят к появлению типичных ошибок. Он полагал, что в процессе изучения нового понятия ученики сосредоточиваются на своем имеющемся опыте, ищут в нем то общее, что связано с новым понятием, связывают новую информацию с тем, что они уже знают. Однако такое предварительное знание не всегда является правильным, что может привести к ошибочному усвоению нового знания.
Работа Р. Эшлока [Ashlock, 2010] по анализу ошибок породила множество аналогичных исследований по всему миру. Было показано, что анализ ошибок является эффективным методом выявления шаблонов математических ошибок для любого учащегося, изучающего математику.
При систематическом анализе детских ошибок учитель получает ряд преимуществ:
— определить, какие шаги ученик выполняет правильно (в отличие от простой фиксации правильных и неправильных ответов, что не дает возможности точно установить правильно выполняемые действия);
— выявить, какие типы ошибок допускает учащийся;
— определить, является ли ошибка случайной, однократной или встречается постоянно, указывая на пробел в освоении математического понятия или алгоритма действия;
— выбрать эффективный подход для устранения проблем учащегося, скорректировать понимание изученных ранее математических понятий, алгоритмов действия [Ashlock, 2010].
К. Лунета и П. Дж. Маконье, в своем исследовании описали различия между математическими ошибками и заблуждениями. Несмотря на то, что эти понятия связаны между собой, тем не менее они имеют разное происхождение. Ошибка — это промах, неточность, несоответствие между объектом или явлением, принятым за эталон [Patterns of Cognitive, 2017]. Согласно Рикомини, бессистемные ошибки являются непреднамеренными, которые учащиеся могут легко исправить сами. Наиболее часто повторяющиеся систематические ошибки являются симптомами ошибочной линии мышления, вызывающей, их и называются заблуждением или ошибочным представлением [Hwang, 2021; Riccomini, 2005]. Характерно, что ошибочные представления интуитивно понятны учащимся, могут быть устойчивы во времени и трудны в исправлении [diSessa, 1993; diSessa, 2019; Misconceptions Reconceived: A, 1994]. Ошибки видны в письменном тексте и устной речи учащихся, но стоящие за ними ошибочные представления часто скрыты от наблюдателя. Иногда они могут быть скрыты даже в правильных ответах, если правильные ответы случайны.
Исследователи университета Северной Каролины отметили, что заблуждения достаточно устойчивы и могут оставаться в течение всей жизни человека. Ошибочные представления имеются и у учителей начальных классов. Даже если учителя знают точный алгоритм вычисления, у них все равно могут оставаться ошибочные представления о некоторых математических операциях (например о том, что сложение и умножение всегда увеличивают число и, наоборот, вычитание и деление всегда уменьшают число) [Green, 1993]. Д. Тирош (D. Tirosh) показал, что ошибочное представление порождается заученным и доведенным до автоматизма алгоритмом действия. Также отмечается, что некоторые учителя начальных классов иногда пропускают тему урока «Деление ноль на ноль», не видят необходимости в этой теме. Это говорит о том, что учитель не владеет базовым пониманием того, что такое деление [Site Quora [Электронный, 2021]. Некоторые исследователи утверждают, что ошибочные представления и заблуждения поддаются исправлению. В настоящее время разрабатываются программы подготовки учителей, нацеленные на преодоление ошибочных представлений у педагогов, а также развитие профессиональных компетенций по организации обучения, основанного на артефактах, организации обучения по формированию математических понятий и развитию математического мышления у учащихся [Green, 1993].
Несмотря на широкое распространение идеи о наличии у детей и взрослых ошибочных представлений, сформированных до систематического обучения, не все исследователи разделяют это мнение. Р. Нешер, Л. Резник и др. считают, что в элементарной математике ошибочные представления возникают только в процессе обучения, поскольку учащиеся обобщают предыдущие знания, чтобы справиться с новыми задачами, но могут делать это неверно [Resnick, 1981].
Основания для типологии ошибок
Вопрос построения типологии ошибок напрямую связан с другим принципиальным вопросом: каким способом ребенок получает знания? Исследования последних десятилетий убедительно доказывают, что способ обучения, основанный на механическом запоминании учебного материала, является неэффективным. В качестве лучших практик называются те, которые поддерживают осмысленное изучение математики, опирающееся на освоение научных понятий [Levin, 2018]. В работах по психологии образования стали обсуждать концептуальные и процессуальные знания. В качестве иллюстрации принципиальных отличий между концептуальными и процессуальными знаниями Ритл-Джонсон предложил следующий пример. Концептуальные знания можно определить как знание концепций, теорий. По сути, они являются абстрактными и необязательно должны быть вербализованы. Процедурные знания могут быть описаны как шаги или действия для достижения цели [Rittl-Johnson, 2015].
Поныне остается дискуссионным вопрос о характере концептуальных и процедурных знаний и их взаимосвязи [Baroody, 2007; Rittl-Johnson, 2015]. В теориях, основанных на идее концептуализации, утверждается, что дети сначала приобретают концептуальные знания, а затем получают процедурные. В теориях, ориентируемых на процедуры, утверждается, что в процессе исследования ребенок осваивает процедурные знания и лишь затем абстрактные концепции. Имеются также ряд работ, в которых показано, что концептуальные и процедурные знания взаимосвязаны и усваиваются также во взаимосвязи [Levin, 2018].
В зависимости от того, как исследователь отвечает на вопрос о способе образования понятий у ребенка, он предлагает способ типологизации ошибок. Так, например, Риттл-Джонсон и Зиглер (1998) считают, что знания, которые ученики должны усвоить первыми, не имеют никакого значения. Другого мнения придерживаются Ортон (1983) и Виннер (1989), которые утверждают, что основная проблема с обучением математическим вычислениям и появлением у обучающихся систематических ошибок заключается в том, что процедурные знания преподаются за счет или до концептуальных знаний [Kakoma, 2021].
Подходы к типологии математических ошибок
Одна из первых типологий математических ошибок была предложена Х. Радацем, в ее основе лежали разные способы обработки информации. Согласно этой типологии, все математические ошибки могут быть объединены в 4 группы. К первой группе можно отнести ошибки, связанные с трудностями понимания математического языка, математического текста. Ко второй группе предложено относить трудности, связанные с пространственным анализом. Третья группа — это ошибки, связанные с трудностями овладения фундаментальными концепциями. Четвертая группа — неверное применение правил, стратегий, решений [Radatz, 1979].
Ряд исследователей предлагали описывать типы ошибок в зависимости от типа математических задач. Например, С. Фиори и Л. Цуккери выявили закономерности ошибок, допущенных младшими школьниками и подростками при выполнении задач на вычитание многозначных чисел. Их классификация ошибок включала ошибки, допущенные при выборе стратегии решения задачи и ошибки вычислений при правильном выборе стратегии решения (например, учащийся допускает ошибку в вычислении 5 - 2 = 2, но остальная часть задачи выполнена правильно) [Fiori, 2005]. Эта типология стала достаточно распространенной и получила развитие. Так, она была дополнена конкретными ошибками, при решении задач с дробями (например, неверно выполненные действия сложения и вычитания дробей с одинаковыми или разными знаменателями и др.) [Effects of Formative, 2021].
Однако не все математические ошибки можно было объяснить неверным пониманием той или иной концепции или применения правил. А. Пэн и З. Ло на основе проведенного анализа литературы, предложили при анализе ошибок учитывать не только сами ошибки учащихся, но и способность учителей интерпретировать эти ошибки. Они считали, что все ошибки образуют четыре группы: математические, логические, стратегические и психологические. Примечательно, что несколько категорий ошибок, предложенных Х. Радацем и А. Пэном, фактически связаны не с математической вычислительной способностью, а с другими областями, такими как язык и визуально-пространственные навыки [Peng, 2009].
М. Клементс, изучая трудности с письменными или устными задачами, отметил, что они иногда связаны не столько с математическими трудностями, сколько с чтением и трудностями понимания языка. Возможно, на овладение умением решать математические задачи влияют не только математические способности, но и другие факторы, например язык, память и зрительнопространственные навыки [Clements, 1980].
По мере того, как в разных странах мира стали разрабатываться новые образовательные стандарты, в которых обращалось внимание на необходимость осмысленного изучения учащимися математики, с учетом роли концептуальных и процессуальных знаний, исследователи начинают более детально подходить к разработке типологии математических ошибок.
Дюфрен (Dufresne) выделил восемь категорий ошибок, которые обычно совершают учащиеся, и определил их следующим образом.
Ошибка в знаниях — недостаточная осведомленность об основных фактах, свойствах или принципах.
Ошибка в навыках — механические ошибки в точности, неправильное копирование математических выражений из одной строки в другую, часто приводящие к неосторожным или «глупым» ошибкам.
Ошибка в концепции — есть недостаток в понимании или неправильное представление.
Ошибка в установлении связей — ученик понимает несколько различных концепций, но ему трудно сформулировать эти концепции вместе, чтобы установить между ними связь и решить задачу.
Ошибка в эффективности стратегии — существует более эффективная стратегия, которая позволила бы за меньшее время прийти к правильному выводу.
Ошибка в соглашении — несоблюдение общепринятых правил, таких как ошибки округления, пропуск единиц измерения и т. д.
Ошибка в процессе — отсутствие каких-либо шагов в решении, таких как определение переменных, указание на применяемые формулы, отсутствие ответа.
Ошибка в формате — написание нелогичных или непоследовательных шагов, некорректное использование знаков равенства, стрелок [Chirume, 2017].
Д. Фишер и Н. Фрей предложили при определении типа ошибок, которые допускают учащиеся, решая математические задания, выявлять шаблоны ошибок. Если учащиеся допускают от трех до пяти ошибок в заданиях определенного типа, это и составляет шаблон ошибки. Так, по мнению исследователей, математические ошибки учащихся можно распределить на три большие группы: фактические, процедурные и концептуальные. Каждая из этих ошибок связана либо с дефицитом знания, либо с недопониманием, неверным представлением. Наиболее распространенным типом ошибок являются процедурные ошибки. Поскольку концептуальные и процедурные знания часто пересекаются, бывает трудно отличить концептуальные ошибки от процедурных ошибок [Visible Learning for, 2016].
Рассмотрим подробнее примеры, иллюстрирующие предложенную типологию математических ошибок [Brown, 2016].
К распространенным фактическим ошибкам относятся следующие.
Ученик не знает базовые математические факты, допускает ошибки при сложении, вычитании, умножении или делении однозначных чисел: 3 + 2 = 7; 2 х 3 = 7; 7 - 4 = 2; 8 : 4 = 3.
Ученик ошибочно идентифицирует знаки арифметических действий: 2 х 3 = 5 (определяет знак умножения как знак сложения); 8 : 4 = 4 (определяет знак деления как знак минус).
Ошибочно идентифицирует цифры: например, 5 идентифицирует как 2.
Делает ошибке при подсчете: 1, 2, 3, 4, 5, 7, 8, 9 (пропускает 6).
Не знает математических терминов (запас слов): не понимает значения терминов: числитель, знаменатель, сумма, прямоугольник.
Не знает математических формул: например, не знает формулу для вычисления площади прямоугольника.
Распространенные процедурные ошибки возникают из-за дефицита процедурных знаний. Процедурные знания — это понимание того, какие шаги или алгоритмы необходимы для решения математического задания. Процедурные ошибки возникают, когда ученик неправильно применяет правило или алгоритм, т. е. формулу или пошаговый алгоритм решения задания.
Например, ученик забывает перенести единицы счета при сложении, вычитании или умножении с переходом через разряд.
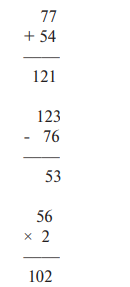
В первом примере ученик правильно сложил 7 + 4, но не перенес единицу в разряд десятков. Во втором примере ученик не занимает единицу в разряде десятков, вместо этого он вычел меньшее число (3) из большего числа (6) в разряде единиц. В третьем примере ученик после умножения 6 х 2 не добавляет единицу к разряду десятков.
Ошибки в случае с одним или несколькими нулями в уменьшаемом.
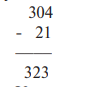
Ученик вычитал 0 из 2 вместо того, чтобы занять единицу в разряде сотен.
Выполнение неправильного действия. Хотя ученик может правильно определять знаки, например, плюс и минус, в то же время он может выполнить вычитание вместо сложения или наоборот.
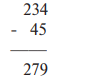
Ученик выполнил сложение вместо вычитания. Или: 3 + 2 = 6 — ученик не прибавил, а умножил. Распространенные концептуальные ошибки возникают, когда ученик придерживается неправильных представлений или не понимает основополагающих принципов и идей, относящихся к данной математической задаче.
Приведем примеры концептуальных ошибок.
Ученик не понимает принципа десятичной записи числа, значения единиц каждого разряда.
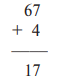
Ученик сложил все числа (6 + 7 + 4 = 17), не различая ценности чисел в разрядах десятков и единиц.

Ученик записал ответ, поменяв в нем местами десятки и единицы. Посмотрим, как ученик выполнил
следующее задание: запишите цифрами числа: 1) семьдесят шесть; 2) девятьсот семьдесят четыре; 3) шесть тысяч сто двадцать четыре.
Ответ ученика: 1) 76; 2) 90074; 3) 600010024.
Ученик при записи чисел, состоящих более чем из двух цифр, демонстрирует непонимание принципа записи десятичных чисел.
К концептуальным ошибкам относятся ситуации чрезмерного обобщения, когда из-за отсутствия концептуального понимания ученик неправильно применяет правила или знания в новой ситуации.
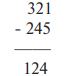
Независимо от того, находится ли число в уменьшаемом или вычитаемом, ученик всегда вычитает из большего числа меньшее.
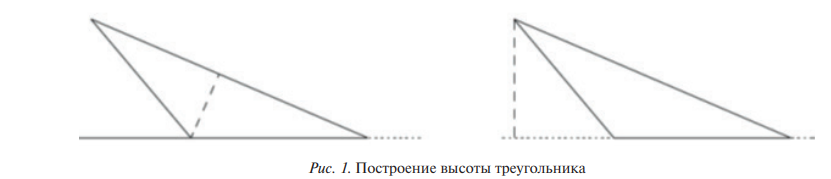
Р. Эшлок [Ashlock, 2010] приводит пример ситуации чрезмерной специализации, когда из-за отсутствия концептуального понимания ученик демонстрирует слишком узкое понимание данного понятия: часто ученики ограничивают свое представление о высоте треугольника только тем, что может содержаться внутри треугольника. Слева показано, как ученик провел высоту к нижней стороне треугольника, справа — правильное построение (рис. 1).
Рассмотренная типология математических ошибок получила широкое распространение и успешно применяется в различных исследованиях, например, при изучении закономерностей ошибок в сложении среди детей дошкольного возраста [Muthukrishnan, 2019], при выявлении шаблонов ошибок учащихся в действиях с обыкновенными дробями [Lestiana, 2016], в задачах сложения и вычитания у португальских школьников [Error patterns in, 2018], при анализе ошибок по математике в начальных классах [Roelien, 2014].
В последнее время разрабатывается еще одно направление в области типологии математических ошибок, когда с ошибками и ошибочными представлениями учитель работает непосредственно в классе. Урок строится в форме учебного диалога, в ходе которого учитель акцентирует внимание учащихся и поддерживает неверное, ошибочное мнение. Эта ошибка обсуждается всеми учащимися класса, подбираются аргументы, почему то или иное мнение, математическое решение является неверным. Так, дети осваивают концептуальное знание. При таком подходе ошибка рассматривается не как неудача, а как важный аспект формирующей оценки, инструментом преодоления ошибочных представлений и более серьезных ошибок в дальнейшем. Однако типология таких ошибок еще только оформляется [Justice, 2020].
Заключение
Данная статья имеет обзорный характер и ориентирована на более глубокое понимание проблемы возникновения основных ошибок младших школьников при освоении математических понятий. Важно отметить, что в современных зарубежных исследованиях существуют разные подходы к типологии математических ошибок. Каждая типология основывается на определенном подходе к обучению, связанном с характером взаимосвязи концептуальных и процессуальных знаний. Исследователи образования придерживаются разных взглядов на процесс овладения учащимися концептуальных знаний. Также нет единого мнения в вопросе о природе ошибочных представлений детей. Дальнейшие исследования могут быть направлены на построение типологии ошибочных математических представлений обучающихся, связанной с детскими ошибками. Одним из перспективных направлений также может стать анализ и отбор лучших практик деятельности общеобразовательных организаций по развитию исходных математических представлений у обучающихся.