Введение
Важнейшим вопросом механики композиционных материалов (КМ) является вычисление эффективных упруго-прочностных характеристик КМ, так как решение данной проблемы позволяет синтезировать материалы с заданным набором свойств, необходимым для конкретных условий эксплуатации конструкций из КМ.
В первых работах, посвященных определению характеристик структурно-неоднородных сред, принимался ряд упрощающих предположений о микроструктуре КМ (Hill, 1963; Hashin, Rosen, 1964; Chamis, 1989; Сенденцки, 1978), таких как предположение о регулярной структуре армирующих элементов, линейной упругости волокна и матрицы, идеальной связи волокна и матрицы, однородности поля напряжений и деформаций, аппроксимация КМ бесконечной средой с расположенным в ней единственным армирующим элементом.
В отдельных работах (Younes et al.; Muyzemnek, Ivanova, Kartashova, 2021) приводится сопоставление результатов вычисления эффективных упругих характеристик с использованием различных аналитических и численных моделей для однонаправленных и тканных КМ. Показано, что для указанного класса КМ, феноменологические, полуэмпирические (Халпина-Цая, Чамиса, модифицированное правило смесей) модели, модель упругого приближения Мори-Танака, двойного включения и мостовая модель позволяют достаточно точно вычислить модуль продольной упругости, однако вычисленные значения поперечного модуля упругости, модулей сдвига, значения коэффициента Пуассона могут отличаться от экспериментально полученных величин и друг от друга в зависимости от выбора расчетной модели на 200%. Неудовлетворительное согласование результатов является следствием достаточно грубых упрощений, принимаемых в математических моделях, а также неидеальной микроструктуры реального КМ.
Для материалов с непериодической структурой используются стохастические подходы, в основе которых лежит теория случайных функций (Buryachenko, 2007; Tashkinov, Wildemann, Mikhailova, 2012; Хорошун, 1978). В работах (Скудра, Булавс, Роценс, 1971; Хорошун, 1968; Kroner, 1967) рассмотрен статистический подход к расчету эффективных упругих характеристик КМ, в основе которого лежит представление компонентов тензора модулей упругости в виде случайных кусочно-постоянных функций координат. Для определения эффективных упругих характеристик КМ системы дифференциальных уравнений теории упругости дополняются корреляционными функциями. Основным преимуществом стохастического подхода является возможность учета статистического разброса свойств компонентов и случайность расположения элементов в структуре. Основным недостатком подхода является невозможность определения корреляционных функций без экспериментальных данных.
Многомасштабный подход
Совершенствование математических моделей КМ предполагает детальное рассмотрение физико-химических процессов, происходящих на границе раздела фаз наполнителя и матрицы, которые могут приводить к изменению характеристик компонентов вследствие их взаимодействия, например образование трещин и отслоений на межфазной границе. К описанию адгезионных процессов на границе раздела фаз существуют 2 подхода: моделирование на основе метода молекулярной физики (Балабаев и др., 1999; Khalatur, 1991) и описание наблюдаемых эффектов как следствия макроскопических воздействий на КМ. При втором подходе межфазный слой может рассматриваться как имеющий геометрические характеристики идеальный слой, или имеющий разрывы полей напряжений и перемещений неидеальный интерфейс. Обзор методов моделирования межфазного слоя представлен в (Соколов, Щетинин, Козлов, 2020; Brosseau, 2024).
При прямом моделировании КМ на микромасштабных уровнях определить свойства КМ представляется возможным только для небольших областей в силу математической и вычислительной сложности таких моделей. Поэтому практически в каждой работе стоит задача гомогенизации, т.е. перехода от структурно-неоднородной среды к эффективной с эквивалентными осредненными упруго-прочностными свойствами.
В процессе гомогенизации производится поиск полей микродеформаций, микроперемещений и микронапряжений, так как характеристики полученные в гомогенном приближении могут влиять на структуру и свойства наполнителя, которые в свою очередь определяют характеристики эквивалентного гомогенного образца.
В работах (Dimitrienko et al., 2023; Schröder, 2014; Geers, Kouznetsova, Brekelmans, 2010; Nguyen, Kouznetsova, Geers, 2012; Lin, Brandyberry, Zhang, 2023) реализованы различные вариации многомасштабного конечно-элементного подхода (FE2) к моделированию КМ, учитывающие взаимное влияние микроструктуры КМ и гомогенного эквивалента КМ. В основе этого класса методов лежит применение теории деформаций к элементарным представительским объемам (RVE), полученным одним из классических методов гомогенизации, постулируется кинематическая непротиворечивость при связывании полей деформаций макроскопического и элементарного представительского объемов под действием внешних поверхностных и объемных сил (рис.1).
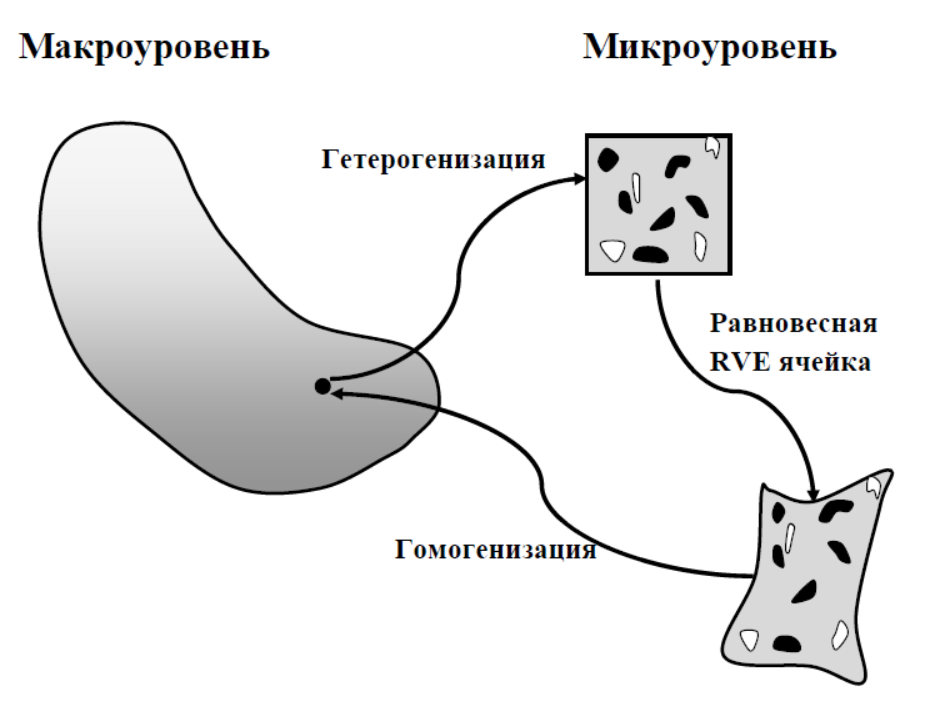
Fig. 1. Multiscale approach scheme
В большинстве случаев для представления гетерогенной среды эквивалентным элементарным объемом (RVE) требуется несколько итераций. Например, в (Blanco et al., 2016; Lopes, Pires, 2022) в рамках многомасштабного подхода исследуется задача определения упруго-пластических свойств КМ, армированного короткими разнонаправленными волокнами. На первом этапе элементарный объем с короткими волокнами заменяются RVE ячейку с единичным однонаправленным волокном на основании подхода Рейса-Фойгта, опирающегося на гипотезу о равенстве напряжений и деформаций в упругопластичных ячейках. На втором этапе гомогенизации усреднение характеристик RVE-объема производится методом конечных элементов. Для получения эквивалентной гомогенизированной среды вводятся ортонормированные базисные вектора для локальной (система координат RVE-ячейки) и глобальной (система координат всего объема КМ) систем координат, с помощью которых определяется матрица трансформации для каждой ячейки. Полученная матрица трансформации участвует в определении компонент напряжений для каждой RVE-ячейки в глобальной системе координат.
В работах (Fish, Shek, 2000; Hashin, 1962) предложен метод введения гетерогенных ячеек периодичности вокруг исследуемой области КМ, получивший название прямой последовательной гетерогенизации (рис.1). Однако существенной проблемой такого подхода является разрыв полей напряжений на границе сопряжения гомогенизированной и гетерогенной областей. В (Белов, 2009) предложен метод «локальных гетерогенизаций», основанный на введении граничного слоя вокруг интересующего слоя толщиной в две ячейки периодичности.
В (Ullah et al., 2020) демонстрируется успешное применение многомасштабного конечно-элементного подхода к моделированию многослойных перекрестно-армированных и квази-изотропных одноосно нагруженных КМ. В (Bruno, 2024) численно моделируется упруго-прочностные характеристики многослойного КМ с дефектами в виде межслойных пустот.
Применение многомасштабного конечно-элементного подхода связано со сложностью согласования пространственно-временных процессов, протекающих на различных масштабных уровнях. На микромасштабном уровне критично описание взаимного влияния матрицы и армирующих компонентов, на мезомасштабе моделируются структурно-морфологические характеристики КМ, на макроуровне – интегральные свойства материала. Сложность описания физических процессов на каждом уровне, необходимость согласования временных масштабов, полей напряжений и деформаций для каждого конечного элемента на каждом временном шаге, влияют на стабильность решения и требуют значительных вычислительных мощностей, что делает данный подход неприменимым для решения практических задач.
Методы построения суррогатных моделей
В последние годы развитие получили методы нейросетевого обучения для моделирования гетерогенных сред, в которых описание физических процессов является затруднительным или не представляется возможным. Основная задача использования нейросетевой модели обучения – замена конечно-элементных моделей суррогатными, основанными на данных.
Для описания характеристик гомогенизированного материала может применяться один из двух подходов. В первом неизвестные коэффициенты функции, описывающей поведение КМ на макроуровне, определяются с использованием экспериментальных данных. Во втором модель КМ на макроуровне строится через определение характеристик КМ на микроуровне, но следует учитывать, что при втором подходе для определения свойств на микроуровне также требуются экспериментальные данные.
Первые работы по использованию нейронных сетей для моделирования макросвойств материалов были опубликованы в 90-х годах (Ghaboussi, Garrett, Wu, 1991; Ghaboussi et al., 1998; Hashash, Jung, Ghaboussi, 2004). Нейронная сеть, устанавливающая соответствие тензоров деформаций и напряжений в двумерной модели, обучалась на основе конечно-элементной модели в двумерном приближении (рис. 2).
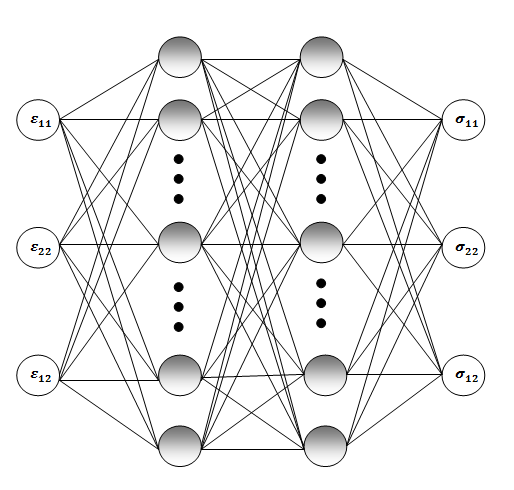
Рис. 2. Установление взаимосвязи тензоров деформаций и напряжений с помощью нейронной сети (серым выделены скрытые нейроны) (Xin, 2020)
Fig. 2. Establishing the relationship between strain and stress tensors using a neural network (hidden neurons are highlighted in gray) (Xin, 2020)
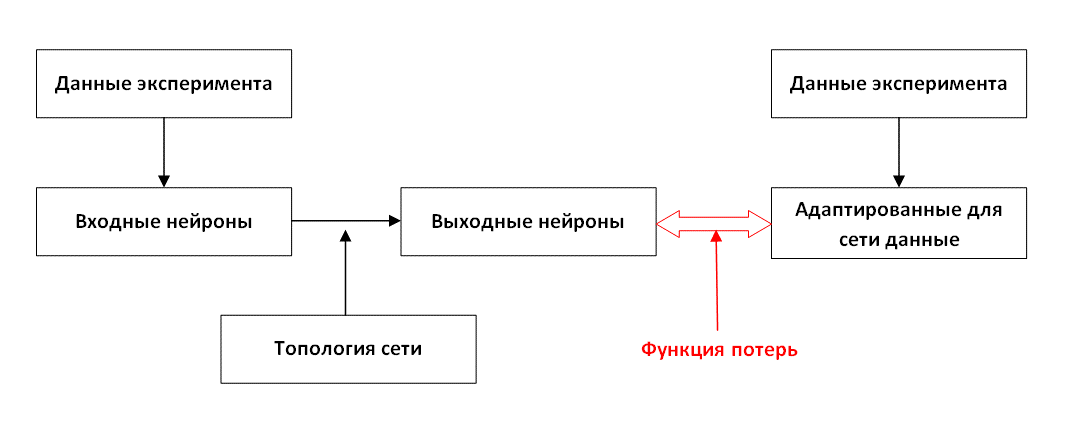
Существует два подхода к обучению нейронной сети. В традиционном методе функция потери строится на основе вычисления и минимизации функции ошибки между полученными с помощью нейронной сети значениями и экспериментальными данными о свойствах материала (рис. 3). Однако такой подход осуществим только, если значения для обучения могут быть измерены с помощью эксперимента.
Рис. 3. Схема обучения нейронной сети на основе экспериментальных данных
Fig. 3. Neural network training scheme based on experimental data
Для обучения нейронной сети необходимо использовать данные о напряжениях, полученные из эксперимента, однако для трехмерных объектов измерение величин напряжений невозможно, также как и их вычисление из-за неизвестности функции зависимости деформаций от нагрузок для КМ. На рисунке 4 показана иная схема обучения нейронной сети: для вычисления данных, которые могут быть получены из натурного эксперимента, используется математическая модель физических процессов, позволяющая на основе данных выходного слоя нейронной сети, рассчитать значения параметров для построения функции ошибки. Основное преимущество данного подхода состоит в том, что на входные и выходные данные нейронной сети не накладываются требования измеримости величин в эксперименте.
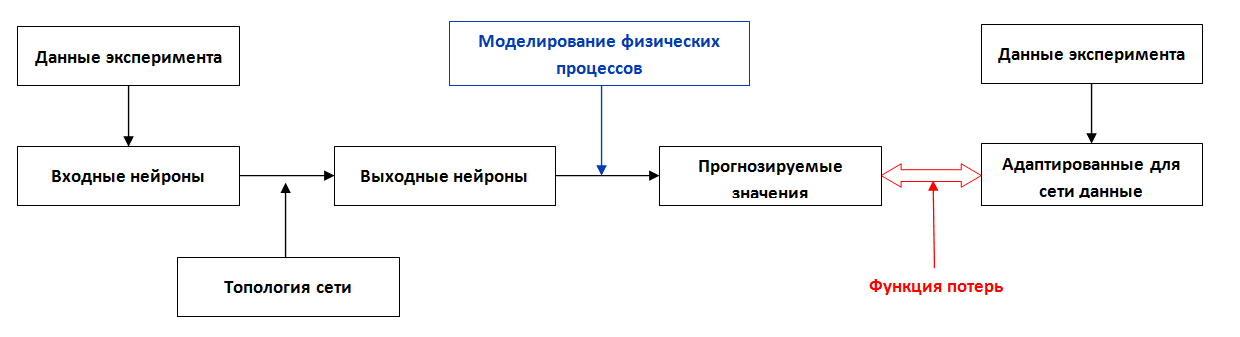
Рис. 4. Схема обучения нейронной сети с предсказательным моделированием
Fig. 4. Neural network training scheme with predictive modeling
Любое многомасштабное моделирование может быть описано уравнением (Xin, 2020)
f(I)=O,
где I – это данные с макроуровня конечно-элементной модели, а O – это значения, полученные в результате моделирования микро и мезо уровней. f может представлять собой как конечно-элементное моделирование, так и любую другую функцию, описывающую изменение состояния в конкретной точке макромодели.
В (Rocha, Kerfriden, van Der Meer, 2020; Deng, 2024; Liu et al., 2024) применена методика моделирования экспериментов DoE (design of experiment), в которой микромеханические характеристики RVE-объемов, находящихся под действием напряжений, передаваемых с макромасштабного уровня, прогнозируются на основе набора аналитических решений задач микромеханики.
В (Dwivedi, Parashar, Srinivasan, 2021) показано, что при моделировании композиционных материалов применение физически информированной нейронной сети (Physics-informed Neural Network) имеет критические недостатки: алгоритм расчета теряет стабильность. Применение физически кодированной нейронной сети (Physics-encoded Neural Network) позволило получить достаточно точную аппроксимацию нелинейной зависимости напряжения от деформаций (Mostajeran, Faroughi, 2024). В (Ghane et al., 2025) для предсказания упруго-пластичных характеристик тканного КМ успешно применена иерархическая физически рекуррентная нейронная сеть (Physically Reccurent Neural Nework).
Заключение
Современный подход к моделированию упруго-прочностных свойств композиционного материала связан с учетом взаимного влияния процессов, происходящих на различных масштабных уровнях структурно неоднородного материала. В связи с тем, что на микро- и мезо- уровнях описание взаимодействия элементов структуры становится более детализированным и требует значительное количество времени для проведения расчетов, то применяемый на макроуровне метод конечных элементов становится малопригодным из-за недостатка вычислительных мощностей. Решение данной проблемы лежит в плоскости применения суррогатных нейросетевых моделей.