Введение
Курсы естественно-научных дисциплин в школе включают в себя знания о мире, его многообразии. В век стремительно развивающихся технологий, глобализации, нестабильной политической ситуации мы сталкиваемся с результатами исчезновения или трансформации биологического разнообразия, нерационального использования природных ресурсов человеком, нарушения экологического равновесия. В свете этого особенное значение приобретает полноценное овладение предметами «биология» и «география» в рамках школьной программы, поскольку именно в школе человек получает первую обобщенную системную информацию о мире, воспитывается понимание взаимозависимости человека и природы, ответственности человека за результаты его деятельности. Олимпиада «Природа России» ориентирована на работу с детьми, проявляющими интерес к данной области. На школьном этапе детям предлагают задания, оценивающие степень ориентации в предмете.
Новизна исследования определяется предложенной моделью количественного и качественного анализа результатов первого этапа олимпиады для использования полученных данных в педагогической работе с детьми, не прошедшими порог оценки. Олимпиадное движение, имея в своей основе выявление наиболее подготовленных в предмете детей, получает инструмент работы с детьми мотивированными, но недостаточно подготовленными.
Материалы и методы
Выборка составила 115 учеников 9-х классов учебных и внеучебных заведений (школы, лицеи, дворцы творчества) ВАО г. Москвы. Олимпиада проводилась в онлайн-формате и была представлена 15 вопросами в рамках предметного материала школьных курсов биологии и географии в 2023/24 учебном году. Условное обозначение вопроса — «V», порядковый номер рядом с буквой обозначает номер вопроса. В исходных данных правильный ответ на вопрос обозначался цифрой 1, а неправильный — цифрой 0. В тексте далее термины «вопросы» и «показатели олимпиады» являются синонимами.
В качестве основных методов статистического анализа были выбраны описательная статистика, корреляционный анализ (Пирсона), кластерный анализ, тепловая карта, построение сетей Изинга, выполненные в языке R (Артеменков, 2021; Гласс, Стенли, 1976; Finnemann et al., 2021).
Результаты
Общий анализ вопросов олимпиады показал, что они все относятся к разным темам и содержательно не связаны. По форме вопросы также отличаются друг от друга. Однако в них можно выделить две разные группы, характеризующиеся одним типом. В частности, девять вопросов требовали дать прямой правильный ответ, а шесть других (V3, V6, V9, V11, V14, V15) были закрытого типа и требовали выбрать один верный из трех имеющихся ответов. Последний тип вопросов предполагает достаточно высокую вероятность правильного ответа даже при незнании предмета. Вопрос об использовании большого количества таких заданий в рамках олимпиады требует дальнейшей более внимательной проработки в соответствии с имеющимися общими требованиями и рекомендациями тестирования (Аванесов, 2014).
В качестве описательных статистик анализировались мода, медиана, среднее арифметическое значение, значение первого и третьего квартилей (Власова и др., 2020; Гласс, Стенли, 1976). Наиболее сложными для детей оказались вопросы 10 и 2 (Mean: 0.1913 и 0.287, нулевое значение медианы, моды и третьего квартиля (3rd Qu.)). Вопросы 4, 12 также имеют низкий уровень успешности прохождения, что отражается в нулевых значениях медианы и моды. Вопросы 13 и 5 отличаются самыми высокими показателями среднего арифметического значения (Mean: 0.9217 и 0.913), первого квартиля (1st Qu.). 92—91 % выборки справились с вопросами 13 и 5 (рис. 1).
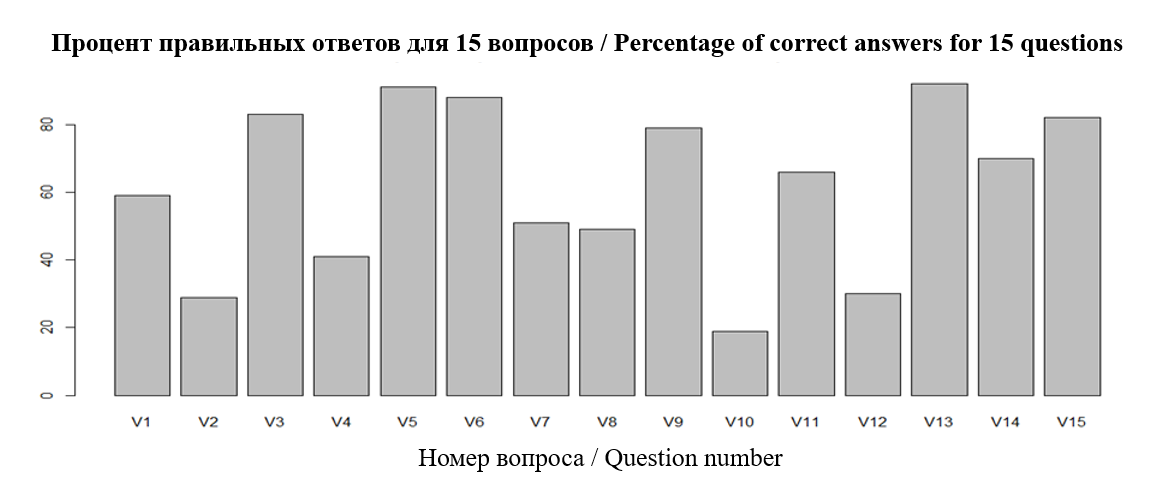
Рис. 1. Диаграмма успешности решения конкретных вопросов олимпиады
(% правильных ответов)
Fig. 1. Diagram of success in solving specific Olympiad questions (% of correct answers)
Остальные вопросы демонстрируют дифференциацию по уровню овладения знаниями в предмете. На все вопросы ответили 7 человек, что составляет 6% от выборки. 42 человека (36%) набрали от 11 до 15 баллов. Результаты 59 человек (51%) находятся в диапазоне от 6 до 10 баллов. От 2 до 5 баллов набрали 16 человек (14%). На рис. 2 показаны общие результаты ответов всех 115 испытуемых.
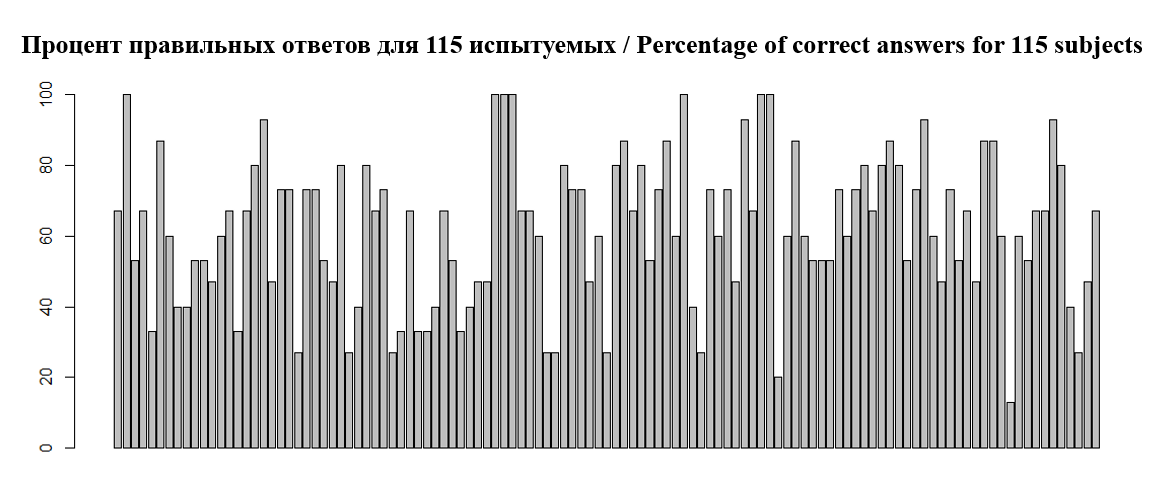
Рис. 2. Процент правильных ответов для 115 испытуемых
Fig. 2. Percentage of correct answers for 115 subjects
Корреляционная матрица тетрахорических корреляций между показателями олимпиады по ответам 115 респондентов обнаруживает в основном положительные связи между показателями (табл. 1).
Таблица 1 / Table 1
Тетрахорические корреляции между показателями олимпиады
Tetrachoric correlations between Olympiad indicators
|
|
V1 |
V2 |
V3 |
V4 |
V5 |
V6 |
V7 |
V8 |
V9 |
V10 |
V11 |
V12 |
V13 |
V14 |
V15 |
|
V1 |
1 |
0,4 |
0,1 |
0,4 |
0,4 |
0,8 |
0,4 |
0,2 |
0,3 |
0,8 |
0,2 |
0,6 |
0.3 |
0,4 |
0,4 |
|
V2 |
|
1 |
0,6 |
0,5 |
0,4 |
0,6 |
0,3 |
0,4 |
0,3 |
0,4 |
0,3 |
0,4 |
0,3 |
0,5 |
0.2 |
|
V3 |
|
|
1 |
0,4 |
-0,2 |
0,4 |
0,4 |
0,4 |
0,1 |
0,4 |
0,1 |
0,6 |
-0,1 |
0,4 |
0,5 |
|
V4 |
|
|
|
1 |
0,5 |
0,5 |
0,4 |
0,1 |
0,6 |
0,4 |
0,1 |
0,6 |
0,3 |
0,5 |
0,4 |
|
V5 |
|
|
|
|
1 |
0,4 |
0,3 |
0,3 |
0,6 |
0,4 |
0,1 |
0,4 |
0,7 |
0,3 |
0,5 |
|
V6 |
|
|
|
|
|
1 |
0,7 |
0,3 |
0,7 |
0,5 |
0,1 |
0,6 |
0,4 |
0,5 |
0,6 |
|
V7 |
|
|
|
|
|
|
1 |
0,3 |
0,3 |
0,7 |
0,2 |
0,4 |
0,4 |
0,4 |
0,4 |
|
V8 |
|
|
|
|
|
|
|
1 |
0,1 |
0,6 |
0,2 |
0,2 |
0,1 |
0,4 |
0,2 |
|
V9 |
|
|
|
|
|
|
|
|
1 |
0,1 |
0,1 |
0,3 |
0,2 |
0,5 |
0,5 |
|
V10 |
|
|
|
|
|
|
|
|
|
1 |
0,2 |
0,8 |
0,3 |
0,6 |
0,6 |
|
V11 |
|
|
|
|
|
|
|
|
|
|
1 |
-0,1 |
0 |
-0,2 |
-0,1 |
|
V12 |
|
|
|
|
|
|
|
|
|
|
|
1 |
0,5 |
0,6 |
0,7 |
|
V13 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0,4 |
0,1 |
|
V14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0,5 |
|
V15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
Тепловая карта отношений между вопросами показана на рис. 3. Большим значениям корреляций на тепловой карте отвечают синие цвета, а меньшим — зеленые. При этом максимальное значение корреляции равно 0,8, а минимальное — 0,2. Кластерное дерево состоит из нескольких ветвей, объединяющих разные вопросы. При смысловом и тематическом анализе вопросов видно, что эти группы различны. В большом кластере одни вопросы объединены в ветки по тематике (V6 и V1 биология — систематика; V7 и V10 — знание предметной номенклатуры), другие по форме вопроса, в частности, определение по фото биологических объектов (V12 и V15); либо по сложности построения вопроса (V4 и V14). В этот же кластер с меньшей значимостью входят вопросы V2, V3 и V8, объединенные общей темой охраны природы. Тогда как в другой ветке вопросы (V5 и V13, V9, V11) отличаются высоким уровнем прохождения, несмотря на то, что востребуют межпредметные знания и, часто, метапредметные навыки (Куравский и др., 2023, Федеральная рабочая программа…, 2022).
Анализ данных показал, что ряд вопросов значительно отличаются по их трудности. Для двух вопросов это можно проверить на основе рассмотрения матрицы 2х2 категорий ответов (0 и 1) с количеством правильных и неправильных ответов респондентов. Например, в табл. 2 представлено количество ответов в каждой из четырех категорий ответов для двух вопросов V1 и V10. Можно видеть, что вопрос V1 оказывается для группы легче, чем вопрос V10 (это также показывает и диаграмма на рис. 1). В частности, нет учеников, которые ответили правильно на вопрос V10 (значение 1), но не ответили на вопрос V1 (значение 0). Эта ситуация приводит к значению тетрахорической корреляции между V1 и V10 равной примерно 0,8.
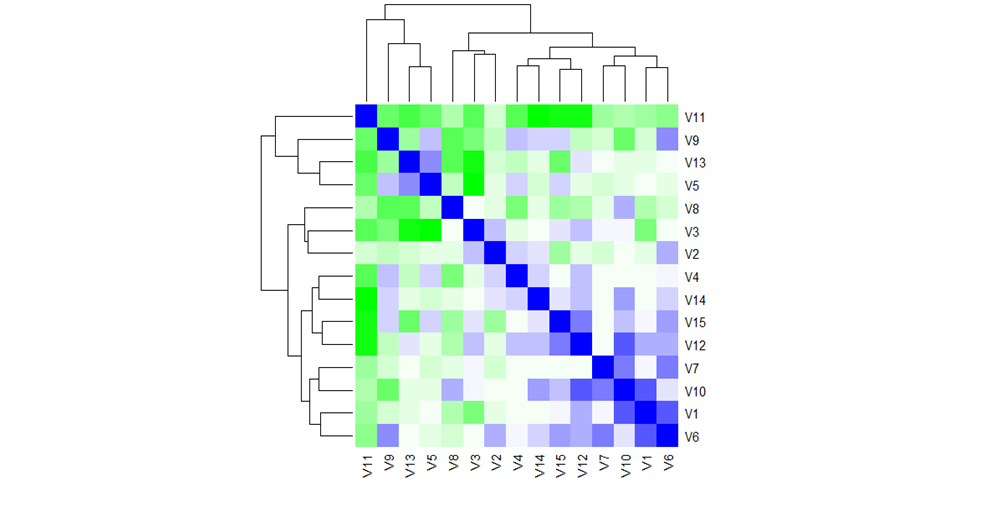
Рис. 3. Тепловая карта вопросов олимпиады с кластеризацией вопросов
Fig. 3. Heat map of olympiad questions with clustering of questions
Таблица 2 / Table 2
Количество ответов в каждой из четырех категорий ответов для вопросов V1 и V10
Number of responses in each of the four response categories for questions V1 and V10
|
Значения / Values |
Вопрос V10/ Question V10 |
|
||
|
0 |
1 |
|||
|
Вопрос V1/ Question V1 |
0 |
47 |
0 |
|
|
1 |
46 |
22 |
|
|
Для того чтобы рассмотреть возможные связи между отдельными вопросами олимпиады, обратимся к графической модели в виде сетевой структуры психологических переменных. Метод сетевого моделирования позволяет визуализировать взаимоотношения между переменными и показывает свою эффективность в современных психологических исследованиях (Артеменков, 2021; Артеменков, Жукова, Богоявленская, 2024; Потанина, Артеменков, 2024; Рубцова и др., 2023). Для бинарных переменных и/или порядковых переменных здесь используется так называемая модель Изинга (Белавин, Кулаков, Усманов, 2001), которая берет свое начало в физике, но часто используется в психометрии, поскольку бинарные переменные распространены в психологических данных (Isvoranu, Epskamp, 2023; Keetelaar et al., 2024; Marsman et al., 2025; Zhang, Chen, 2024). Эта модель определяет распределение совместных вероятностей по имеющимся двоичным переменным.
На рис. 4 представлена сеть Изинга, полученная на основе применения пакета IsingSampler в языке R. Алгоритм в этом пакете представляет собой нерегуляризованный метод оценки сети и фокусируется на изучении разреженных сетевых структур при наличии скрытых переменных с помощью подхода выпуклой оптимизации. Результирующая сеть приближенно показывает наиболее выраженные связи между вопросами. Мы видим, что 8 вопросов (V1, V2, V5, V6, V10, V12, V13, V15) образуют сеть с высокими положительными связями. С содержательной стороны — это по большей части вопросы, требующие определения природного объекта по описанию, рисунку или фотографии. Остальные 7 вопросов (V3, V4, V7, V8, V9, V11, V14) отличаются отсутствием больших связей между собой и предыдущей группой и характеризуются большей сложностью для группы. Объединяя биологические и географические понятия, их решение востребовало не столько память и знания, сколько мыслительные операции, принятие решения в ситуации сопоставления множества условий, метапредметные навыки.
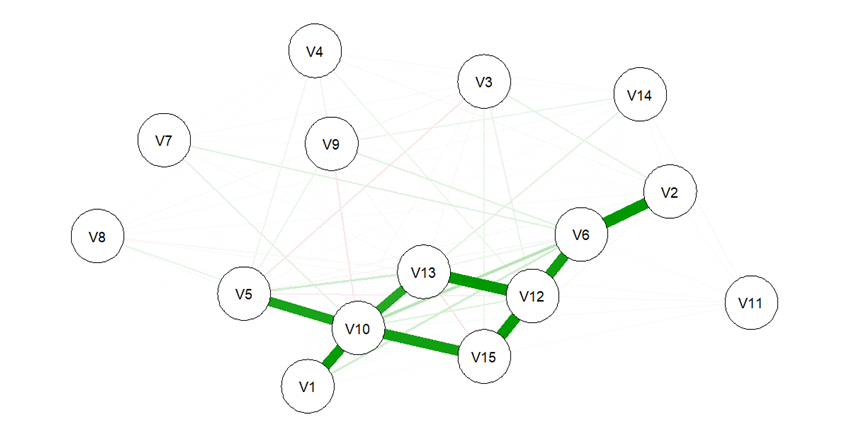
Рис. 4. Общий вид сети Изинга между ответами на вопросы олимпиады
Fig. 4. General view of the Ising network between the answers to the Olympiad questions
Другой метод построения сети Изинга, представленный в пакете IsingFit, делает упор на статистическую обработку исходных данных и байесовский вывод (Finnemann et al., 2021; van Borkulo et al., 2014). IsingFit использует форму регуляризации eLasso (предполагая разреженную базовую сеть). Результирующая разреженность сети Изинга зависит от гиперпараметра γ, который задается в диапазоне 0—0,5.
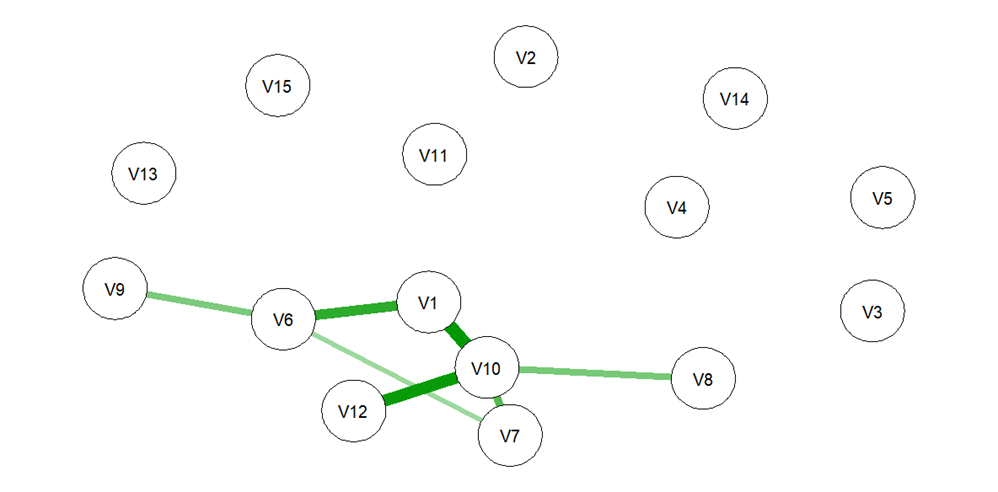
Рис. 5. Общий вид регуляризованной сети Изинга между вопросами олимпиады (γ = 0,25)
Fig. 5. General view of the regularized Ising network between the Olympiad questions (γ = 0.25)
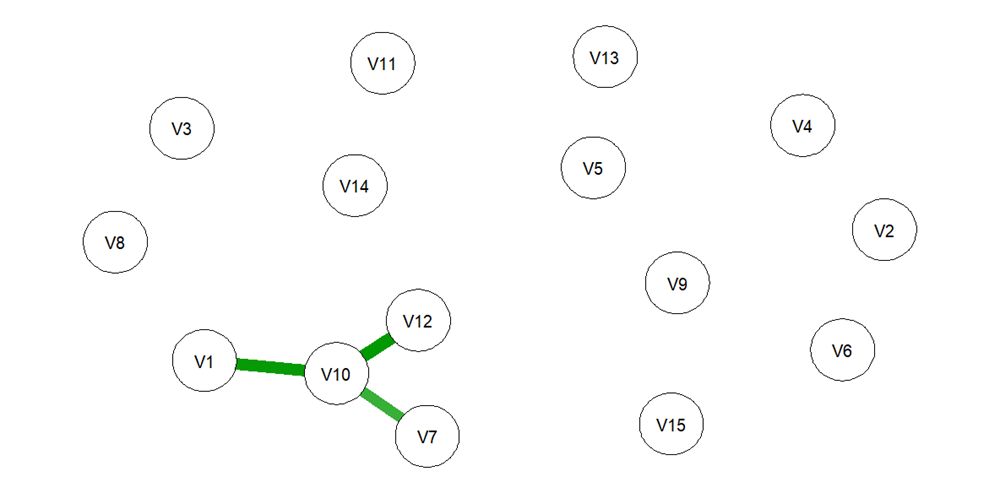
Рис. 6. Общий вид регуляризованной сети Изинга между вопросами олимпиады (γ = 0,5)
Fig. 6. General view of the regularized Ising network between the Olympiad questions (γ = 0.5)
На рис. 5 и 6 показаны регуляризованные сети Изинга, построенные для двух разных значений γ. Можно видеть, что с увеличением гиперпараметра γ разреженность сети растет.
Использование метода eLasso сжимает оценки связей между многими отдельными узлами сети до нуля, что увеличивает количество отсутствующих ребер. Результирующая разреженность сети отчасти облегчает ее интерпретацию, поскольку остаются только самые важные ребра (van Borkulo et al., 2014). В частности, на рис. 6 остались только 3 самых сильных ребра, характеризующие связи вопроса V10 с вопросами V1, V7, V12. Эти ребра соответствуют самым большим тетрахорическим корреляциям: для V1 — 0,79, для V7 — 0,7, для V12 — 0,77.
Обсуждение результатов
Известно, что на ответ влияет как предметное содержание, так и форма вопроса на олимпиаде. Можно утверждать, что наличие вопросов закрытого типа в целом повысило успешность ответов испытуемых. Средняя успешность ответов на вопросы закрытого типа составила 90%. В то время как средняя успешность ответов на другие вопросы составила 69%. В целом математический анализ позволил дифференцировать вопросы олимпиады по степени сложности и охарактеризовать уровень овладения материалом в разных разделах предмета. Результаты олимпиады наглядно показывают проблемы в работе с тематическими текстами и терминологией, включенной в содержание школьных предметов, трудности определения объекта по визуальному образцу.
Сетевой анализ связей между вопросами, выполненный на основе построения регуляризованных сетей Изинга для имеющихся бинарных переменных, показал, что основное количество вопросов оказалось не связанными друг с другом. Это отражает как их содержательную несвязанность, так и разную степень овладения отдельными темами или разную успешность в понимании тех или иных вопросов. Ряд обнаруженных достаточно больших корреляционных зависимостей между отдельными показателями оказался вызван наличием плохо решаемых вопросов, в частности, наиболее трудным оказался вопрос V10, относящийся к определению вида растения, которое не было узнано почти у 80% участников. При этом эти участники были много лучше в других вопросах. Таким образом, можно утверждать, что найденные корреляционные связи образовались не столько в результате тенденции совместного лучшего знания, сколько по принципу совместного незнания ряда вопросов у достаточно большого числа участников, т. е. связи между заданиями здесь образовались в результате наличия согласованного незнания. Это позволило нам выделить пробелы в овладении базовыми понятиями биологии и географии у детей данной возрастной группы.
В рамках предложенных заданий в ряде случаев тяжело происходило определение объекта по фотографии. Эти задания требовали определить особо охраняемые природные территории (ООПТ) и объекты России, вид растения или животного. Для такого распознавания требуется лучшее знание учащимися конкретного материала, что говорит о важности проведения практических работ, выездных биологических практик. Необходимость знакомства с живыми объектами в реальности, а не опосредованно, отмечается многими педагогами (Сапарбаева, 2019; Рохлов, Петросова, 2022; Романова, 2018).
Заключение
Проведенный анализ позволил дифференцировать задания по форме, степени сложности, определить темы и характер вопросов, вызывающих наибольшие трудности, рассмотреть особенности восприятия и понимания детьми предложенных заданий. В качестве первичной рекомендации к составлению заданий олимпиады можно указать на необходимость лучшей оптимизации заданий олимпиады по их трудности.
В результате были выявлены проблемные области в освоении биологических и географических знаний детьми 9-х классов. Можно говорить о необходимости работы по применению предметных знаний на практике, использованию учебных задач, основанных на межпредметных связях, развитию умений применять географические и биологические знания как рабочие инструменты.
Полученные результаты интересны с точки зрения оптимизации образовательных технологий в современной старшей школе (Жукова, Баранов, 2020; Лазарев, Хайбуллин, 2014; Романова, 2018; Сапарбаева, 2019; Рохлов, Петросова, 2022; Шмигирилова, Рванова, Григоренко, 2021). Предложенная форма анализа результатов может быть использована в рамках методической работы в школе как инструмент внешней оценки педагогической практики, повышения предметной подготовки школьников (Евстафьева и др., 2020), качества разрабатываемых олимпиадных заданий. Представленный сетевой анализ позволил выявить имеющиеся пробелы в овладении базовыми понятиями биологии и географии.
Качественная оценка результатов может стать психолого-педагогическим ресурсом дифференцированного подхода к определенной группе — мотивированных детей, находящихся в стадии становления предметного знания. Отсутствие поддержки этой категории может приводить к потере мотивации к предмету. Бережное ведение детей на пути раскрытия их потенциала — одна из главных проблем педагогического знания.
В качестве перспектив дальнейших исследований выступают вопросы оптимизации управления процессом подготовки школьника в рамках предметного знания. Получение обезличенной информации о качестве результатов проходного этапа олимпиады позволит исключить стихийность подготовки школьника и поддержать категорию детей, наиболее мотивированную в предмете.
Ограничения. Наборы данных хранятся у организаторов олимпиады «Природа России» и не подлежат опубликованию.
Limitations. The data sets are stored by the organizers of the Nature of Russia Olympiad and are not subject to publication.